角の二等分線に関する重要な3つの公式 D D とおく。 AB=a, AC=b, BD=d,DC=e, AD=f AB = a,AC = b,BD = d,DC = e,AD = f とおくとき以下が成立する。 公式1は辺の比の公式で教科書にも載っています。 公式2は暗記する必要はありませんが,導出方法は覚えておくとよいです角の二等分線と比 教材を発見 正8面体の頂点巡り (1) 三角柱の展開図;角の二等分線上は、2辺からの距離が等しくなる。 という特徴がありましたね! 〇辺から等しい距離に ときたら、角の二等分線を使うようにしてください。 詳しくはこちらの記事でも解説しています。

角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
角の二等分線 線分比
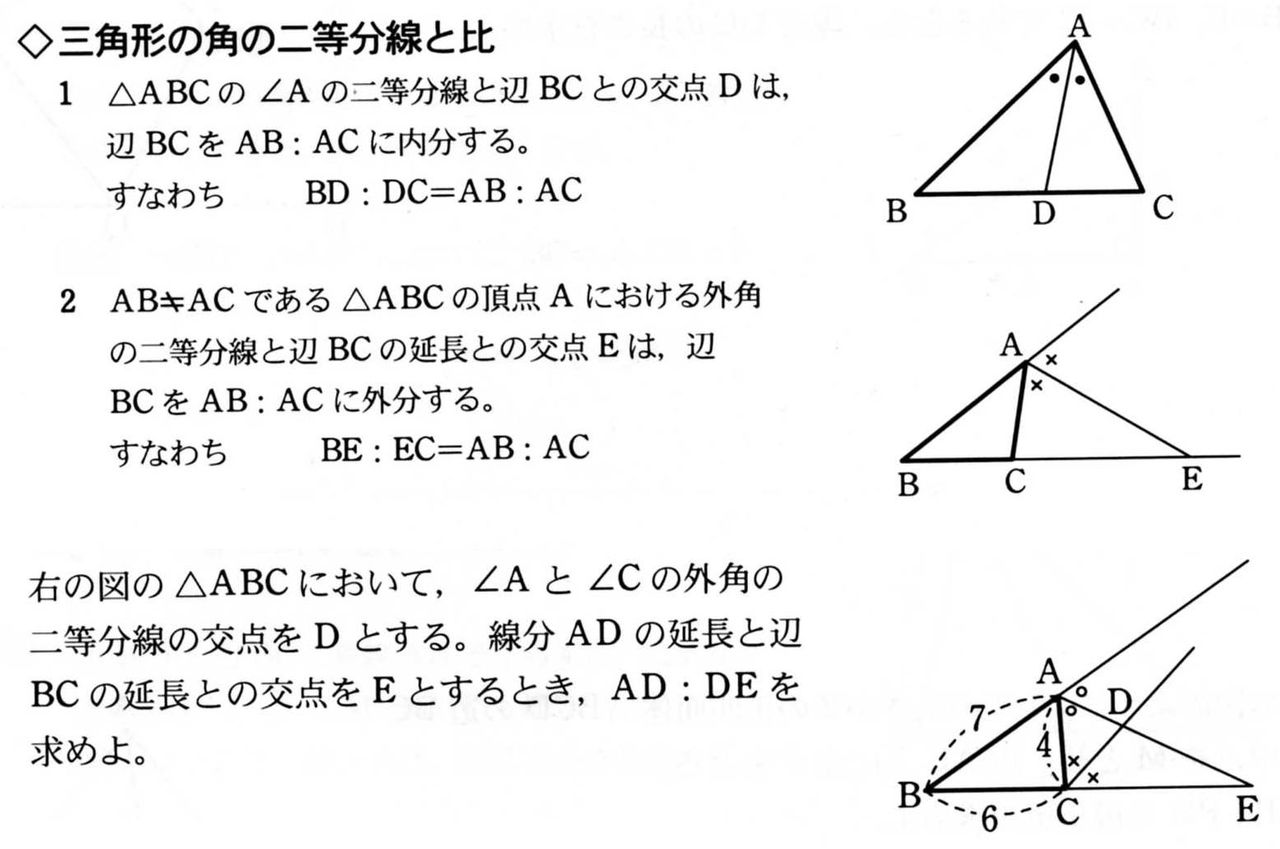
角の二等分線 線分比- 辺の比の関係式は内角の二等分線とまったく同じなので、別々に暗記する必要はありません。 ただし、二等分線と向かい合う辺の交点の位置が 元の \(\triangle \mathrm{ABC}\) の外側にある ことに注意しておきましょう。 角の二等分線の性質⑶ ceの長さを求めよ。 角の二等分線と比 abcにおいて adが∠a の二等分線のとき aeが∠a の外角の二等分線のとき bd:dc = ab:ac be : ec = ab:ac a b d c 6 4 5 a b d c mn m n a c n m b n e 高1・高2 数 ス 第18講 recri oding スのの スの・




三角形の面積 応用 角の二等分線 Youtube
三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内三角形の角の二等分線 と比(1 時間) 〈目標〉 三角形の頂点の2等分線からわかることを調べ,既習内容 を使って証明しようとする。 問題 三角形の紙を,頂点の角を2等分するように折ると, 折り目と底辺の交点はどんなところにありますか? 直線qt, ruをそれぞれ引いて線分abと交わった点が3等分点(・)である。 証明は平行線と線分の比を使えば出来るのかと思います。証明は今回は載せていません。 こんな感じで任意の線分の3等分はできます。もちろん 等分もできるんじゃね?と思っております。
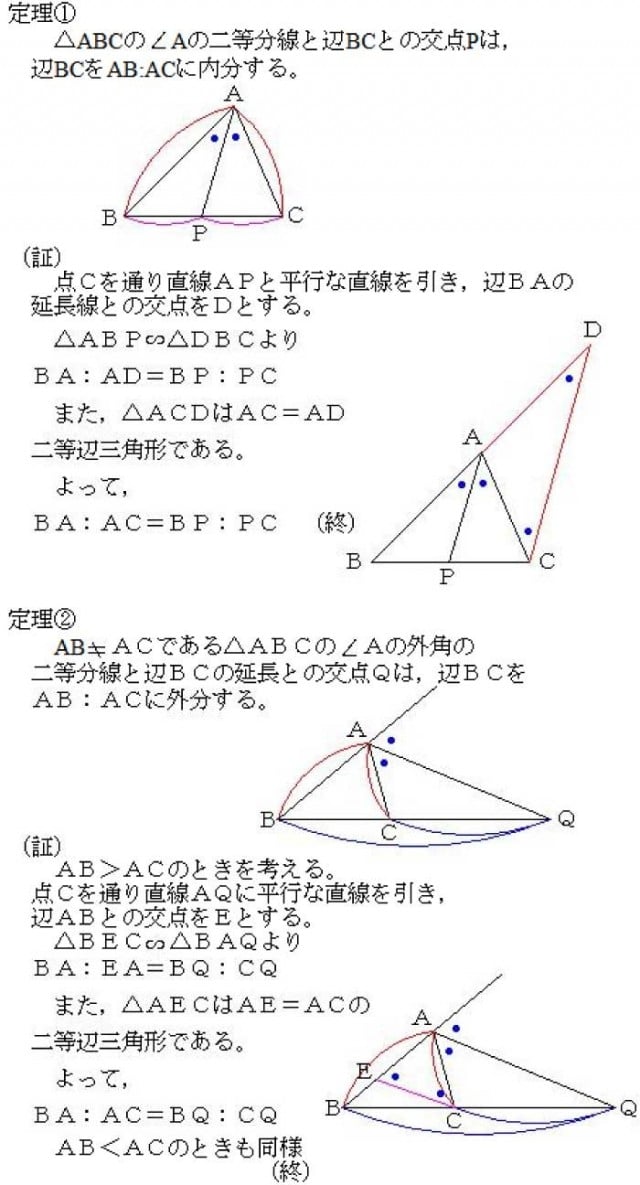
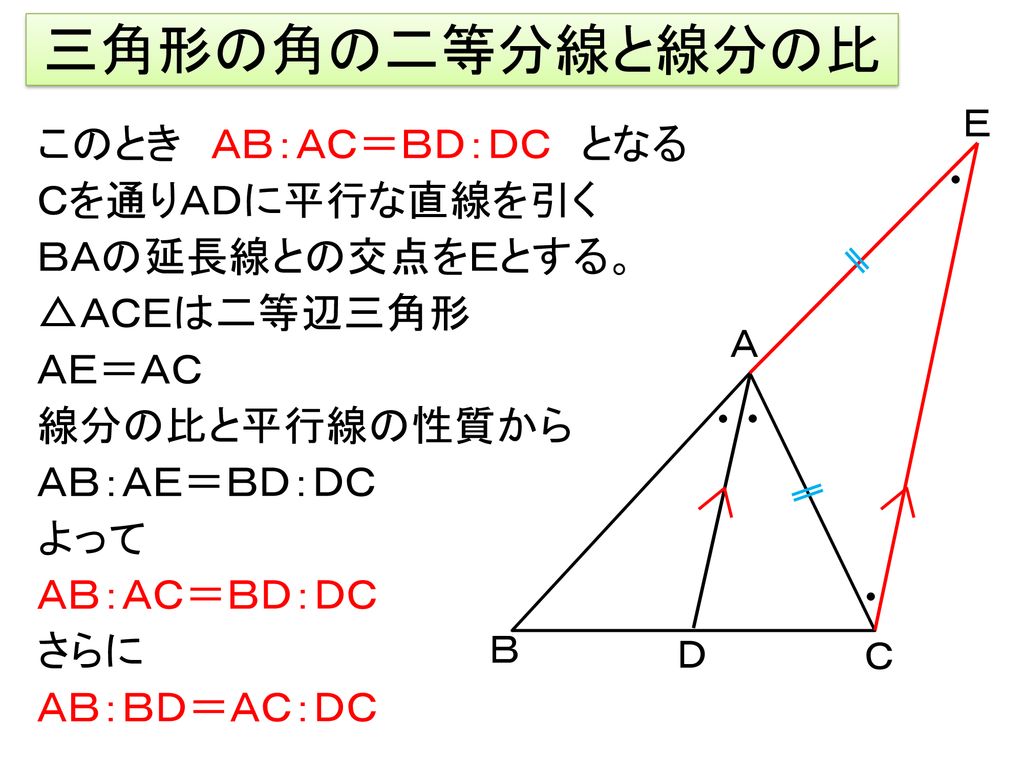
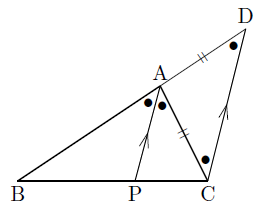
角の二等分線に関する定理としては,次のものはよく知られているかと思います~ BD:CD の比が AB:AC と等しいことを利用して AD の長さを求めるというのが 基本的な解法パターンになってますよね。 では,その AD の長さを与える公式を与えてみましょう(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。 つまり、「線分の二等分線」は1つだけではなくいくつも存在することが分かります。 また、下記のように線分と垂直に交わる二等分線を垂直二等分線と言います。こちらの方が聞き馴染みがあります。 角の二等分線 角の二等分線を知っていますか?
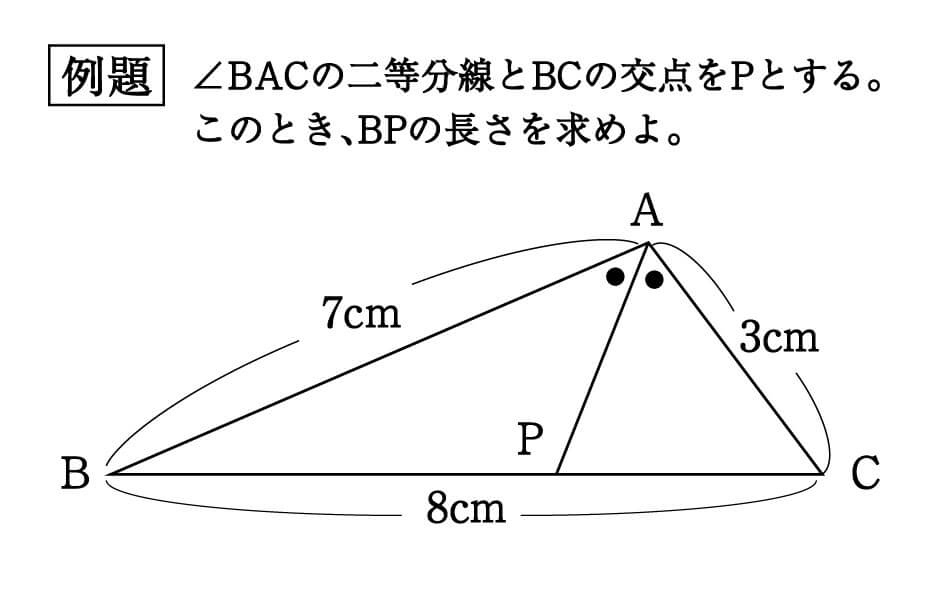
1上の三角形で,ap=5,pb=2,aq=4,pq= 25 のとき,qc とbc の長さを求めよ。 角の二等分線と線分の比 4abc の頂角a の二等分線は,対辺bc を ab ac の比に内分する。 a b d c m m n n 例題 6 a の二等分線がbc と交わる点をd としたとき,bd の長 さとdc の長さを求めよ。 a 上野竜生です。今回は角の二等分線と線分比の公式を紹介します。外角バージョンも紹介します。 角の二等分線の性質 図においてad,afは∠bac,∠caeの二等分線である。このとき (1) abac=bdcd (2) a 最後に、平行線と線分の比から $$\begin{eqnarray}ABAE(AC)=BDDC \end{eqnarray}$$ となります。 まとめ! お疲れ様でした! 内角の二等分線と比の性質は入試でもよく出題されます。 なので、絶対に覚えておきたいですね。



中学三年数学の 三角形の角の二等分線と比 の問題です Ab Ac Yahoo 知恵袋
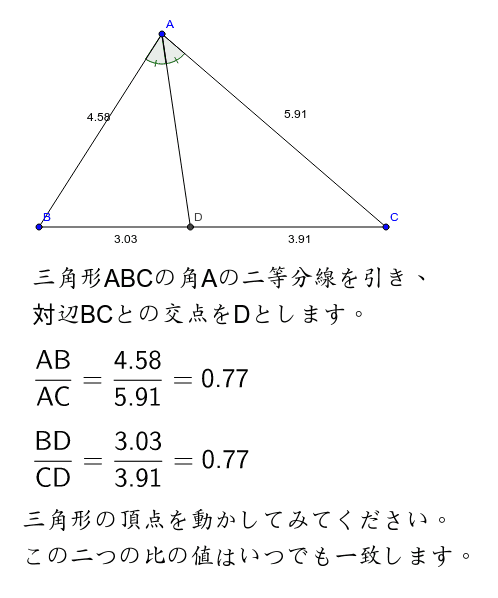



三角形の内角の2等分線と対辺 Geogebra
角の \(\boldsymbol{2}\) 等分線と線分比 このときの 角の \(\boldsymbol{2}\) 等分線と対辺の交点との関係 を見ていきます。 下図のように、 頂点 \(C\) を通り、\(AD\) に平行な直線を辺 \(AB\) の延長と交わるように引き、その交点を \(P\) とします。角の二等分線の長さの公式 である。 このとき、 が成り立つ。 (追記) 平成24年2月11日付け 数学の研究会で、開成高校の木部先生が、角の2等分線の長さの公式 を紹介された。 角の二等分線の長さ 三角形の内角・外角の二等分線の性質は,中学数学で習う基本的で重要な性質です.それらの主張とその証明を紹介します.さらに,後半では発展的内容として,角の二等分線の長さについても紹介します. ⇨予備知識 角の二等分線




高校数学b 角の二等分線のベクトル2パターン 受験の月
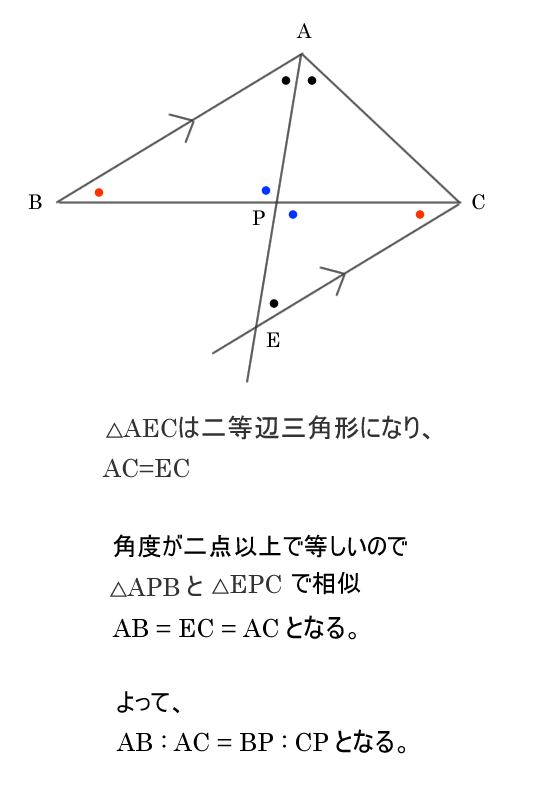



角の二等分線定理 証明 優技録
$\angle \mathrm{ A }$ の値がわからないので、基本三角比と角の二等分線のように面積を使って解くのは難しいです。 しかし、同じページ内でも復習した「 $\mathrm{ AB }\mathrm{ AC }=\mathrm{ BD }\mathrm{ CD }$ 」という角の二等分線に関する性質は使えます。 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか・二等辺三角形の等辺を挟む角の二等分線は、対辺の垂直二等分線である。およびその逆。 ・ある線分の両端と、その線分の垂直二等分線上の任意の点で、三角形が出来るとき、 それは二等辺三角形である。 ・中点連結定理 などは、既知のこととします。
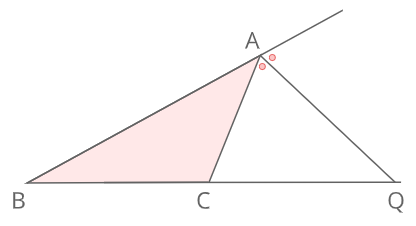



高校数学 外角の二等分線と比 の公式とその証明 Enggy



長さの比 角の二等分線の定理 浅野中学 13年 どう解く 中学受験算数
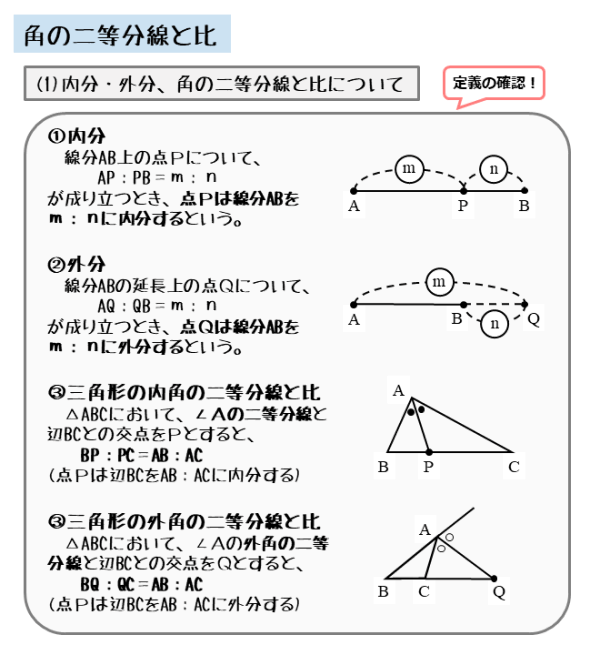
"内角の二等分線と比"の公式とその証明です! 内角の二等分線と比公式内角の二等分線と比 ∠aの二等分線とbcの交点をpとすると \(bp:pc=ab:ac\)証明①三角形の相似による証明証明 cを通りapに平行な線とabの延長との交点 "外角の二等分線と比"の公式とその証明です! 外角の二等分線と比公式外角の二等分線と比点aの外角の二等分線とbcの延長との交点をqとすると \(bq:qc=ab:ac\)証明①三角形の相似による証明証明 cを通りaqに平行な線とa知っておくと役に立つ以下の定理があります。 角の 2 2 等分と線分の比 下図のように、角 A A の 2 2 等分線と、 BC B C の交点を D D とします。 このとき、 BD DC = AB AC B D D C = A B A C 一応、中学数学の範囲外なので、頻繁に出題されるものではありませんが
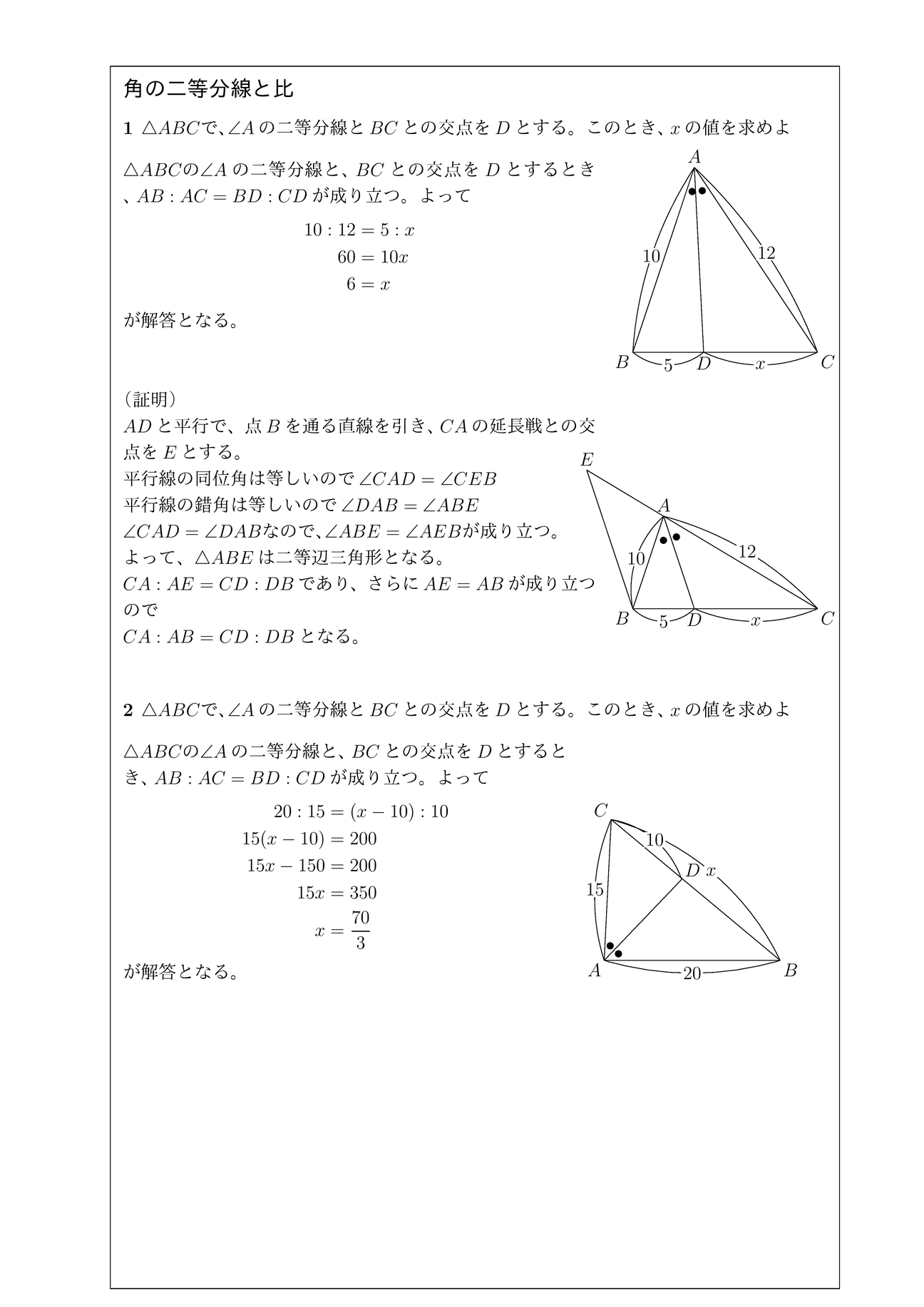



角の二等分線と比 チーム エン
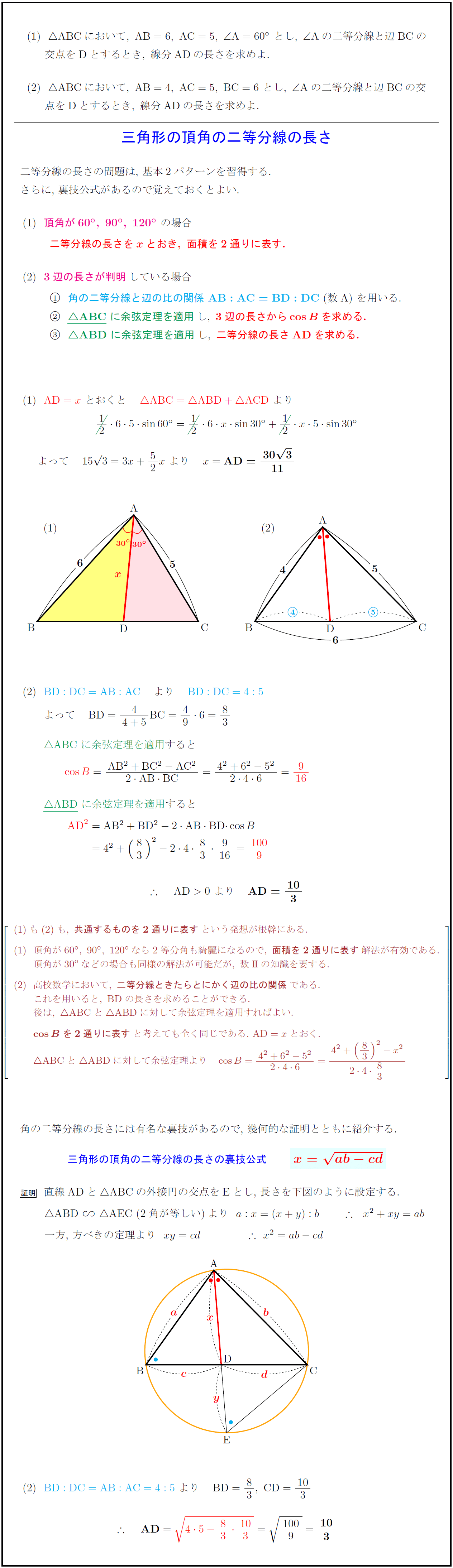



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




角の二等分線と比 おいしい数学
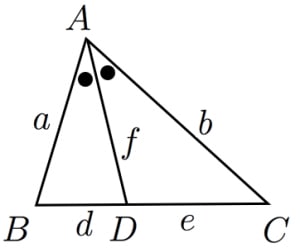



角の二等分線に関する重要な3つの公式 高校数学の美しい物語
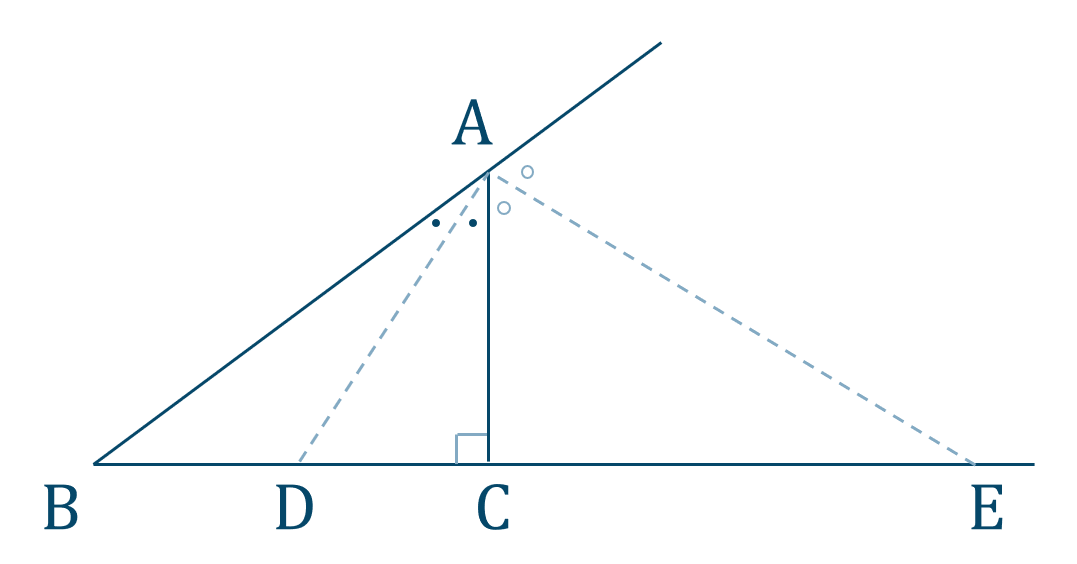



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学
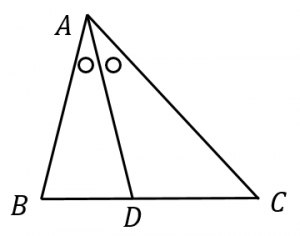



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
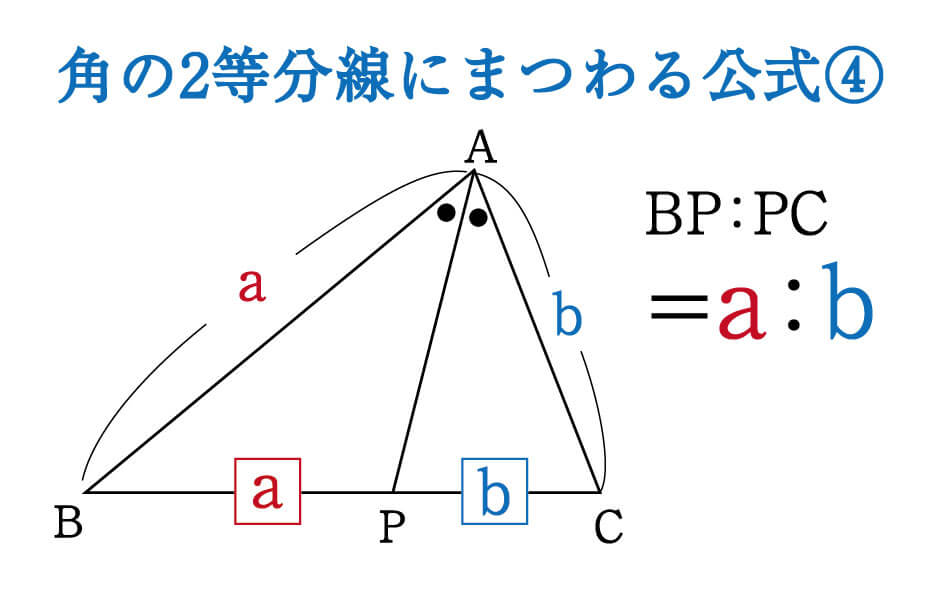



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学3年生の相似な図形 角の二等分線と比に関する問題です 以下の写真 Yahoo 知恵袋




数学aの三角形の角の二等分線と比の問題についてです 1からさっぱりわ 数学 教えて Goo




基本 角の二等分線の作図 なかけんの数学ノート




基本 三角比と角の二等分線 なかけんの数学ノート



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext
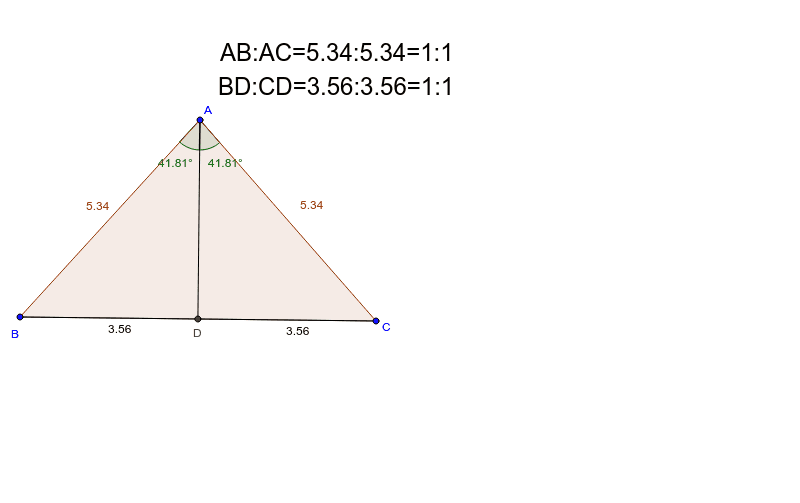



角の二等分線と線分の比 Geogebra



角の二等分線の定理 中学入試 高校入試 算数 数学質問所
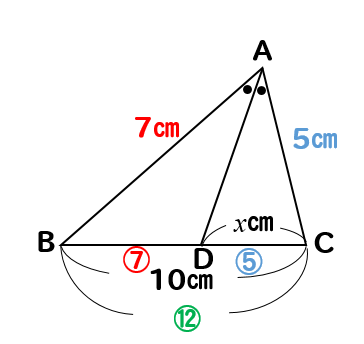



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



外心




受験数学かずスクール 三角形の角の二等分線の定理の解説 図形的な意味は面積の比



中3数学 角の二等分線定理のポイントと練習問題
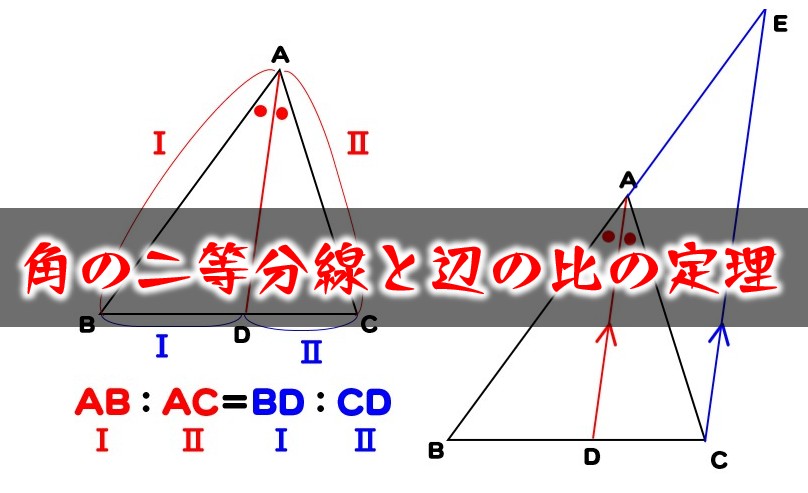



角の二等分線と辺の比 の証明 問題の解き方 数学fun




角の二等分線に関する定理 高校数学の知識庫



三角形の角の二等分線と比




中3 19 1三角形の角の二等分線と線分比 Youtube




角の二等分線定理の証明 学びをつづる



平行線と線分の比 中学3年 数学クラブ




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
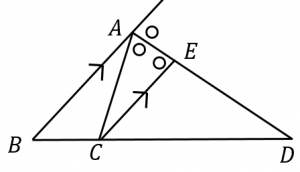



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア
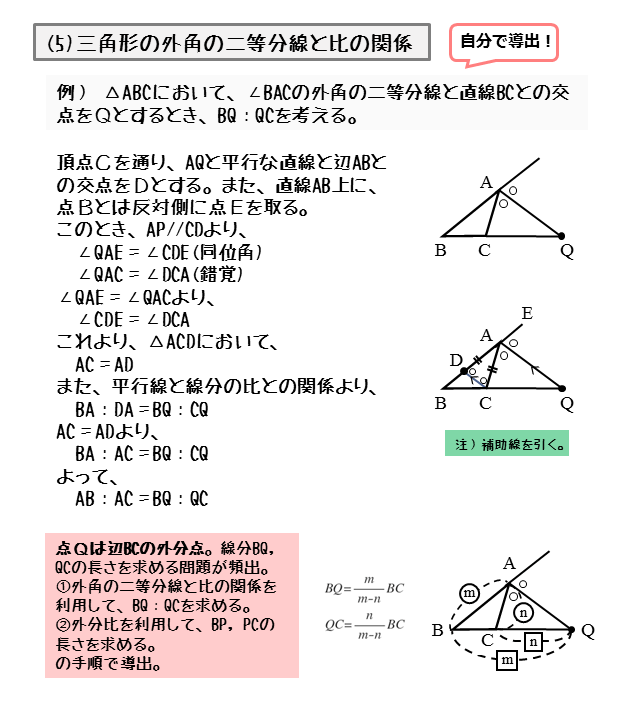



図形の性質 角の二等分線と比について 日々是鍛錬 ひびこれたんれん



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



高校入試数学 面積比のポイントと練習問題
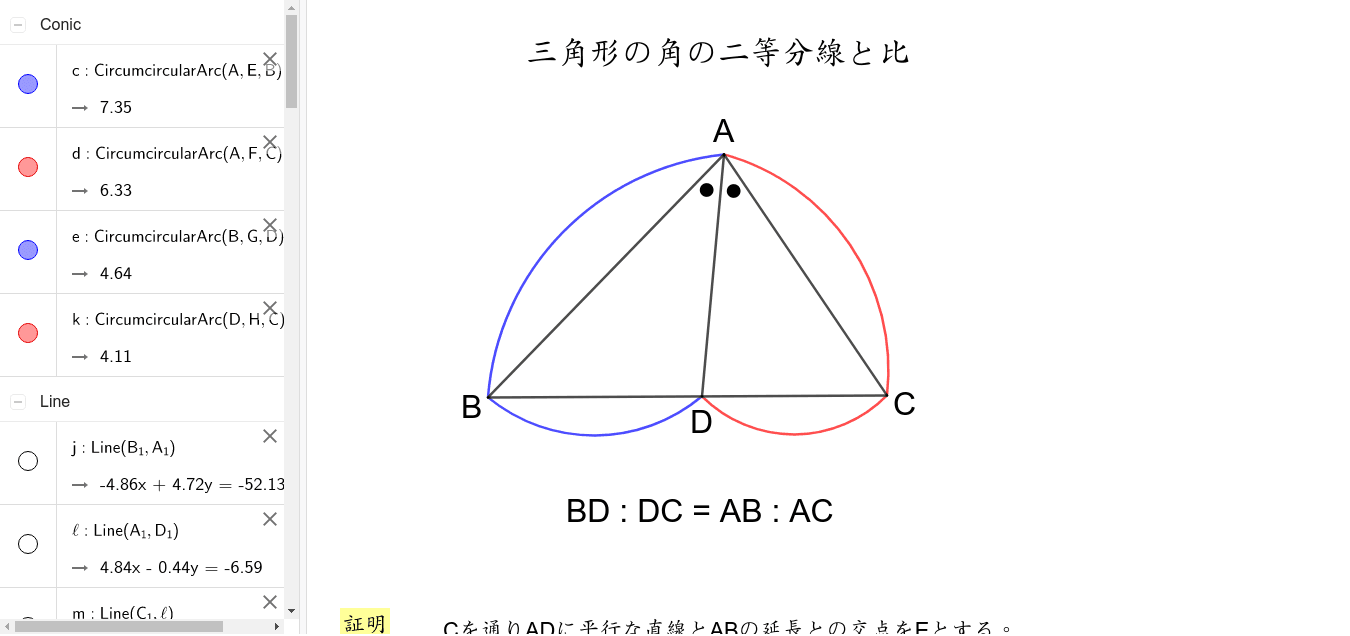



三角形の角の二等分線と比1 Geogebra




角の2等分線の性質を用いた長さおよび比を求める問題について 人力検索はてな



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



第5章15 相似の応用 三角形の角の二等分線と線分の比 フロントエンドなブログ




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の面積 応用 角の二等分線 Youtube
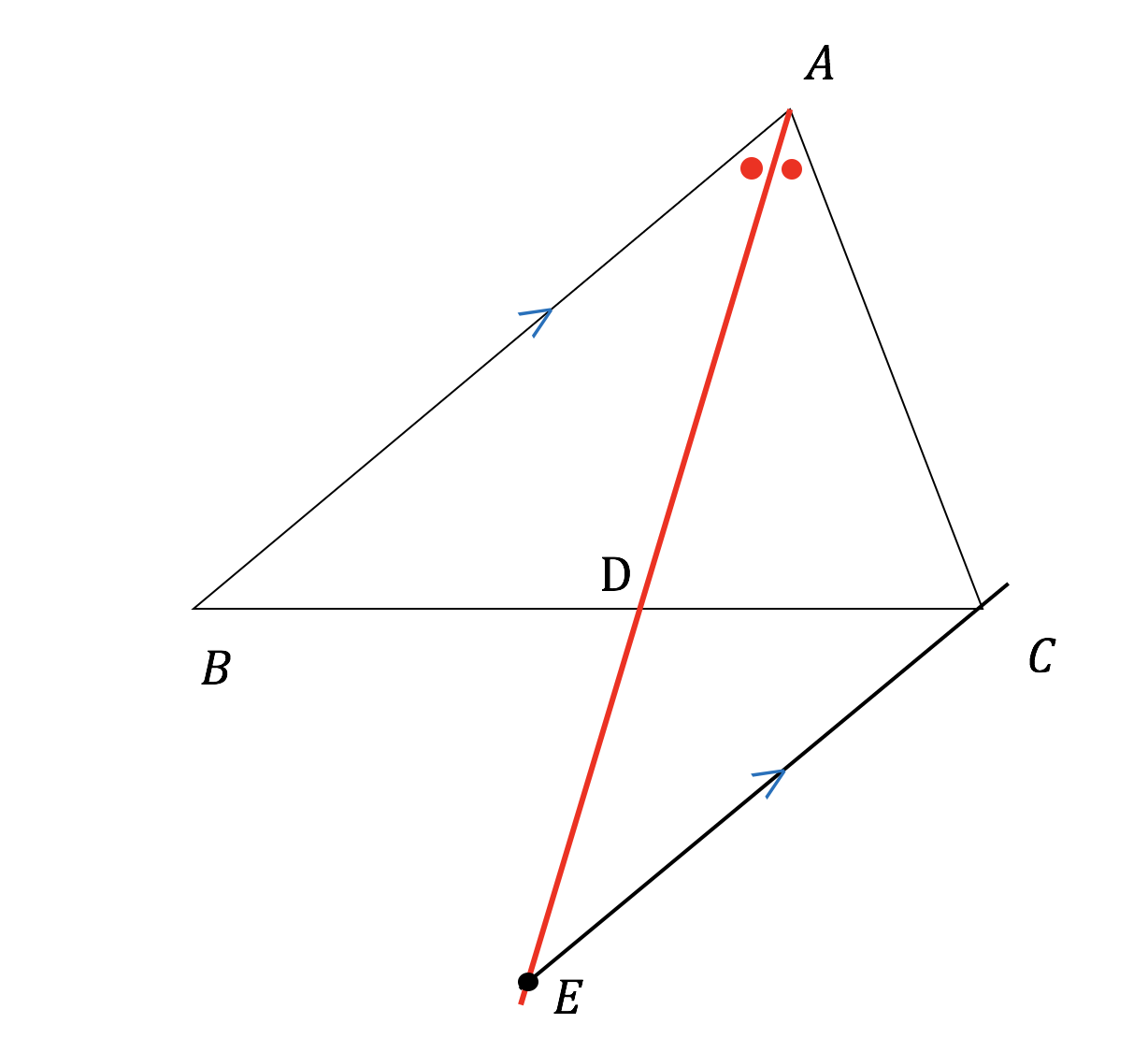



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ




角の2等分線によって分ける比 身勝手な主張




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




角の二等分線と比 おいしい数学



Tossランド 角の二等分線と線分の比 の基礎 基本
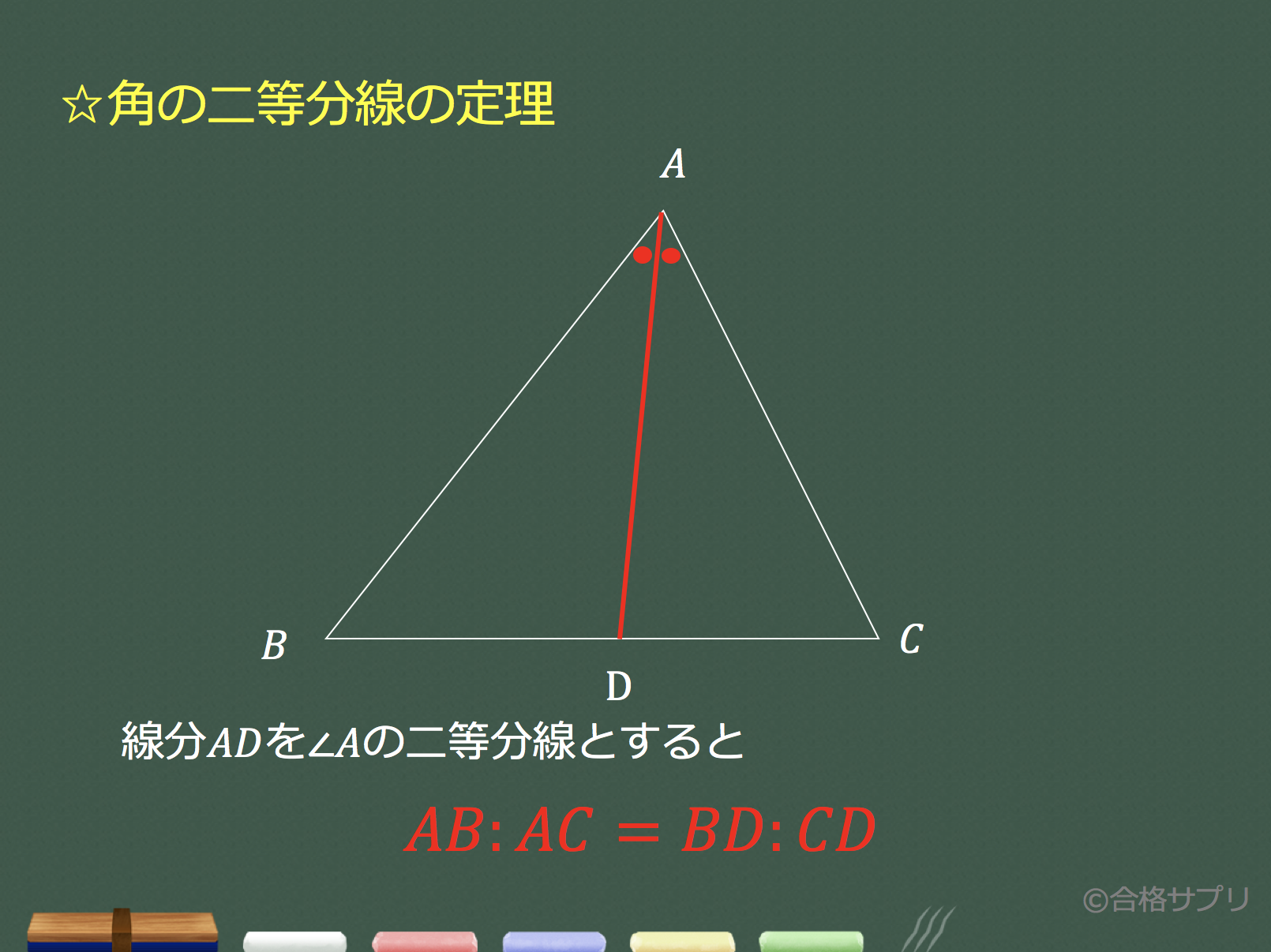



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ




勉強しよう数学 角の二等分線の長さ 相似図形による定理の証明



Koki 角の二等分線 74 Powered By Line



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



三角形の角の二等分線と比




高校生 角の二等分線のノート一覧 Clearnote




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



三角形の角の二等分線定理



傍接円 傍心について



中3数学 角の二等分線と線分比 2 Youtube




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



傍心 ぼうしん とは 東大合格コム



1



角の二等分線




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext



本時のねらい 三角形の1辺に平行な直線が他の2辺と交わるとき それぞれの交点は その2辺を等しい比に分けることを理解する Ppt Download




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




頂角の二等分線が底辺を分割するときの比に関する問題 大垣日大高校入試問題より 身勝手な主張




角の二等分線の長さを導出する4通りの方法 理系のための備忘録



内角の2等分線と線分の比 まなびの学園



1




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角の二等分線と比 おいしい数学




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext



角の2等分線の長さ




高校数学a 角の二等分線と比の利用 例題編 映像授業のtry It トライイット



三角形の角の二等分線定理 外角



2




内角の二等分線 外角の二等分線の比の定理 証明 Youtube
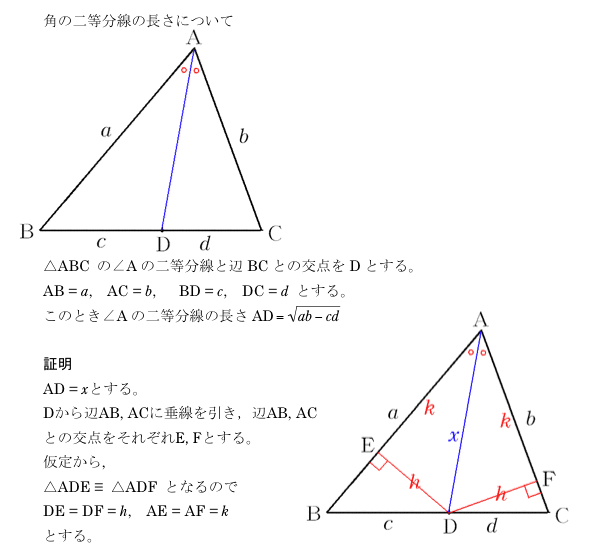



角の二等分線の長さ Takapの数学日記
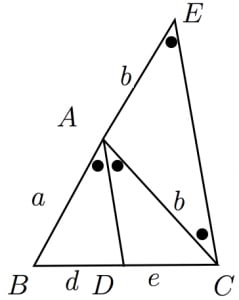



角の二等分線に関する重要な3つの公式 高校数学の美しい物語




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



内接円 内心
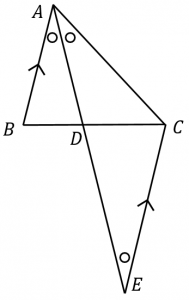



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学
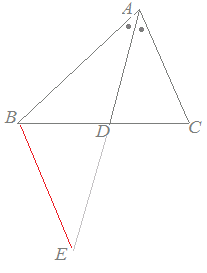



角の二等分線と補助線




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット
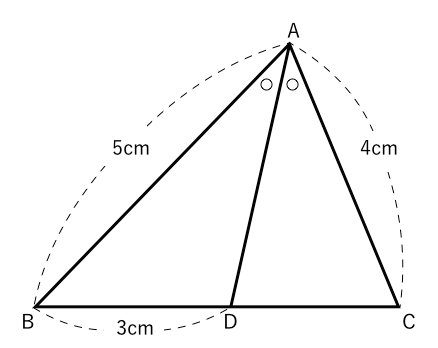



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に



角の二等分線の定理の逆 大学受験の王道
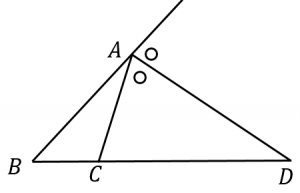



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



角の二等分線に関する問題 中学受験 田中貴 Com




どことどこが相似なのでしょうか Clearnote



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



数学aの問題です 次の図において Apは Aの二等分線である Yahoo 知恵袋
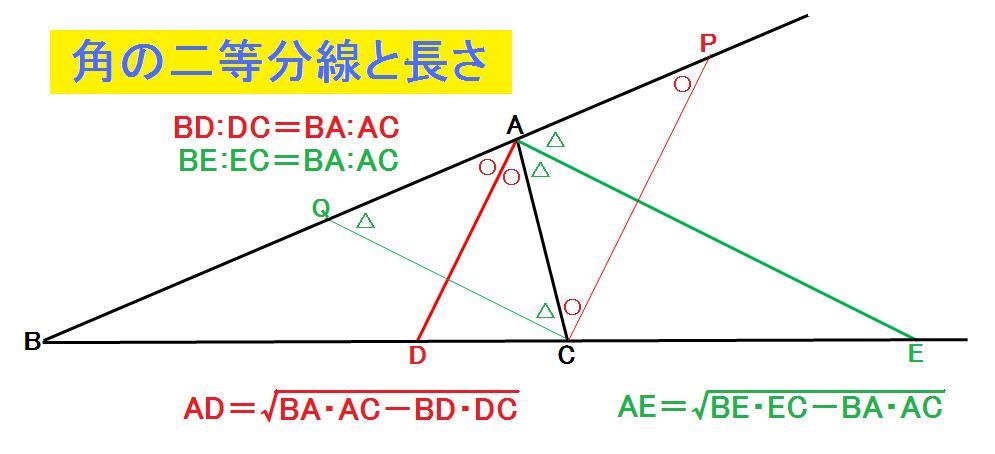



角の二等分線の長さの公式 算数 数学記事




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿