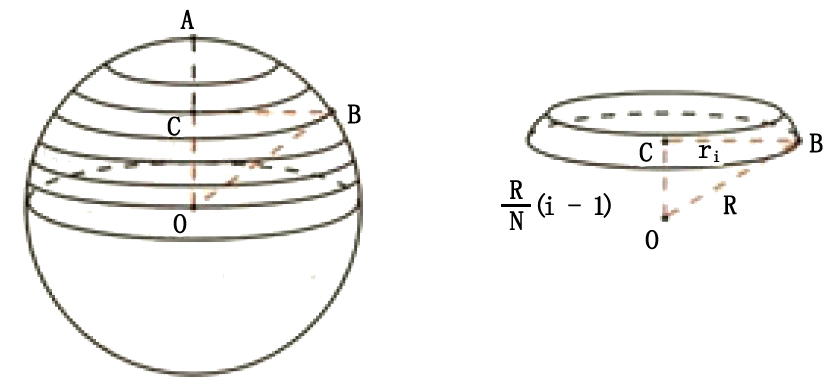
円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデアが出現する。 上野(09)は「測る」というテーマに着目して, 多角形や円の面積,多面体や回転体の体積を求めるた めに必要な極限概念,カヴァリエリの原理,積分概念『球の体積』より V = 4 3πr3 なので 4 3πr3 = 1 3Sr ∴ S = 4πr2 である。3 表面積 図2 タマネギ状に切る 3 と同様に、n 次元単位球の表面積Sn から求めよう。図2 のように球を 同心球によってタマネギ状に切り分ける。dt を十分小さくとると斜線部分の 体積は (半径t のn 次元球の表面積) dt となる。下線部分はSntn 1 となるから Vn
腾讯视频
球 体積 表面積 なぜ
球 体積 表面積 なぜ-演習0002 N 次元球の体積と表面積 M H Nakano 12 年6 月 日 1 問題 N 次元ユークリッド空間において jxj2 = XN i=1 (xi)2 = r2 (1)で定められる対象が半径r のN 次元球の表面であり, jxj2 = XN i=1 (xi)2 • r2 (2)を満たす領域が半径r のN 次元球である。 これらの表面積SN(r) と体積VN(r) を求 めよ。 ヒント:次元 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A = πr2 A = π r 2 の式において、 r2 r 2 の 2 2 を



圆球表面积 球体表面积的公式证明 篆体字转换器
三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64( c m 3 ) となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2 輪切りの考え方から, 球体の表面積=円柱の側面積 ∴ 球体の表面積=円柱の側面積= 4πr2 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め
一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波球の体積 110 /79件 表示件数 5 10 30 50 100 0 1 26 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 前立腺はくるみ大といわれるが、一般的なくるみのサイズで半径15cmで計算してみたら14強になり、前立腺肥大の閾値が>mLなの 球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を切って得られる立体の名前 球欠,球台の体積 球冠,球帯の表面積
この状態で、2つの球の半径の差 $ \Delta r $ を限りなく 0 に近づけると、2つの球の表面積の差はほとんどなくなりますね。このとき、球殻の体積は、(半径 $ r $ の球の表面積 S)× $ \Delta r $ で求められるのです‼(← ここがポイント!球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 「球の体積」については覚えなくていい「円の面積」 算数は得意なのに数学が苦手なひとのためのブログを見てみてください。 mynkit 1912 覚えなくていい「球の表面積・体積」



Q Tbn And9gcr4yydsanpcv9odoui8ies6cbemi 5dfwxzcqjdm Pjn0r0 Ymu Usqp Cau




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
⑵ 球と円柱の表面積の比を「球:円柱」として表せ。 149 次の図のよ う な立体の体積と表面積を求めよ 。 ⑴ 半球 ⑵ 球の 1 4 ⑶ 半球と円柱を組み合わせた立体 学基本学習の基本 35 球の体積と表面積よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.




1 6 球的表面積與體積 Mathtsing高中數學 Youtube



写给5年级的学生 球公式是如何推导出来的 表面积
うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめてい②球の表面積の公式の求め方(1) 次に、球の表面積の公式の求め方について考察する。 まずは体積のときと同様にすると、図1において、 球の中心から距離 x の点で切った断面である円の 円周の長さは、 2 -x 2) となる。 よって、球の表面積Sは、円周を x7、球の表面積 T:ところで、球の体積がわかると、球の表面積もわかる。 s:球は曲がっているのに、表面積が求まるんですか。 T:夏になるとスイカを食べるだろ。あのスイカを食べやすくするために切るね。そのスイカ をどんどん小さくしていく。する




體表面積表初中數學 幾何 面積與體積公式 Uhlwc



球的表面积公式 球的表面积公式画法
球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚え込みだけで得 た知識は,定着が悪く,応用も効きにくくなります。単元「空間図形」の小単元「球の表面積と体積」(2時間)における数学的活動を取り入れた授業展開案です。 単元 空間図形 (啓林館) ・ g ・ 球の表面積と体積(移行措置に伴う補助教材) 全2時間 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




用感覺理解球體表面積公式 Youtube
球の体積=4 3πr3 球 の 体 積 = 4 3 π r 3 なので、 4 3π63 4 3 π 6 3 = 2π = 2 π 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 なので 4π62 4 π 6 2 = 144π = 144 π 半球の体積を求める方法 元の球の状態の体積を求めて半分にしてやります。 \frac {4} {3}\pi \times 3^3=36\pi 36\pi \times \frac {1} {2}=18\pi (cm^3) まぁ、半球だからといって特別な公式があるわけではありませんね! だけど、表面積はちょっと注意が必要です。 球の体積の求め方は\ (\frac {4} {3}\pi r^3\) であり、これを覚えてしまえば、半径を代入するだけで求められる。 少々覚えづらい公式かもしれないが 表面積は「面積」なので2次元の世界→よって二乗 体積は3次元の世界→よって三乗 と考えておくと多少覚え




積分球公式球的體積 Jvvx



球表面积公式推导图解 搜狗图片搜索
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の表面積と体積1 名前 次の式を書きなさい。 3# ①半径 の球の体積 を求める式。 4# ②半径 の球の表面積 を求める式。 32 次の球の表面積と体積を求めなさい。 cm 表面積: 体積: cm 表面積: 体積: 右の図は、半径が cmの球を、中心を通る平面で切って球の体積と表面積について 新潟県立阿賀黎明高等学校 西條和久 平成14年11月29日 1 はじめに 来年度より,新学習指導要領が実施され,いくつかの中学校の内容が高校へ移行する。




球的表面积和体积公式是什么 球体的表面积 体积公




球體表面積球體 表面積 體積 Vhjk




球的体积 表面积 简书



高中数学必修2教案 1 3 2 球的体积和表面积 淘文库



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili



球體表面積球體 表面積 體積 Vhjk




科學月刊 大小有什麼差別 上




球的表面积第1页 驾考预约大全



在球的体积公式中 为什么会出现三分之四这个奇怪的



球的体积和表面积公式怎么算球的表面积和体积 自媒体热点




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



高考数学考点之空间几何体的表面积和体积 王羽课堂



细品教材 从生活经验中我们知道 不能将橘子皮展成平面 因为橘子皮近似于球面 这种曲面不能展成平面图形 那么 人们又是怎样计算球面的面积的呢 古人在计算圆周率时 一般是用割圆术 即用圆的内接或外切正多边形来逼近圆的周长 理论上 只要圆内接正多边形边




高中数学必修二经典考题 球的表面积和体积 含答案 三好网



圆球体积公式 球的体积和表面积 趣闻趣事网



球体体积公式 怎样计算球体的体积



球的表面积公式和体积公式 微页高考网




圆锥与球与圆柱




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



椭球 维基百科 自由的百科全书




球体积公式




球相交的表面积并 体积并 Jzk Keven 的博客 Csdn博客



球的表面积与体积 哔哩哔哩 つロ干杯 Bilibili




球の体積と表面積 Youtube




外接球体积的常见套路 几何 知乎



球的体积表面积 扒拉扒拉
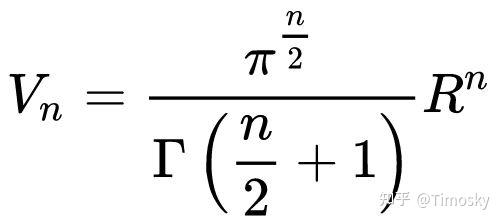



球的表面积最大 球的表面积公式推导 圆台体积公式




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



腾讯视频




012 球的体积空间几何体高中数学 Youtube



球体积的前世今生 新华网



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球体积公式表面积推导过程是什么多少计算公式 小街网




球面積積分球的體積 Itha




球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條




球缺体积和球冠表面积的计算公式及应用 台部落




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




球体体积 球体表面积公式 球体体积公式 简明教程




球的体积与表面积 简书




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



Qy6jpildnxafom



球的体积公式和表面积公式 高三网



球的体积及表面积公式 Ppt 360文库



1
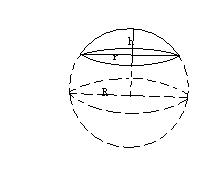



球缺 维基百科 自由的百科全书



1




球表面積公式球體表面積 百度百科 Kmbymh



圆球体积公式 球的体积和表面积 趣闻趣事网




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球体的表面积和体积的计算公式 星火网校



圆球表面积 球体表面积的公式证明 篆体字转换器




球表面積計算球的體積 Jlxpis




高中数学必修二经典考题 球的表面积和体积 含答案 三好网




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org



球冠表面积公式 快懂百科



常用体积计算公式 电子工程世界



圆球表面积公式推导球体的体积公式 表面积公式的推导
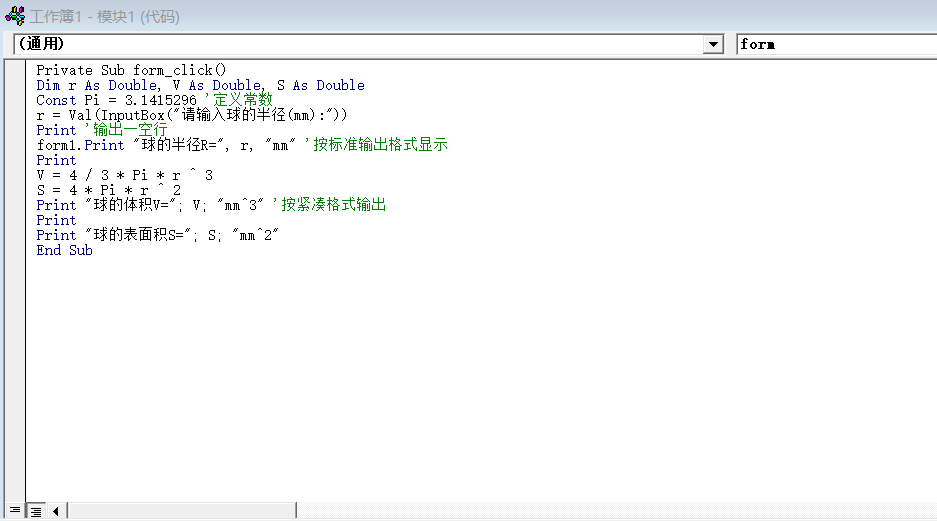



Vb实验 计算球的体积与表面积 隔壁老王521的博客 程序员宅基地 程序员宅基地




球的表面积和体积怎么算啊怎么计算球的表面积




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球冠体积 表面积在线计算器




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球表面積球的體積 Qrv Co



球的表面積的求法 中學數學課 隨意窩xuite日誌




表面积公式球



微积分计算球的表面积如何推算出球的表面积



球體體積 總表面面積 Youtube




求球体的表面积和体积 修也 Csdn博客



球冠表面积计算公式 圣恩灵修网



当圆柱容球时 球的体积 时习社区




牛客小白月赛 C 关于球相交的表面积和体积并 牛客博客



球的表面积公式推导 万图壁纸网



球的体积和表面积ppt免费下载 第一ppt




球的表面积公式是什么 球体积 表面积公式是



圆球表面积 球体表面积及体积的推导 趣闻趣事网




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org




球表面積公式球體表面積 百度百科 Kmbymh



圆球表面积 球体表面积及体积的推导 趣闻趣事网



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社



表面积体积公式大全 搜狗图片搜索



试题3 1 3空间几何体的表面积与体积 1 3空间几何体的表面积与体积 高中人教a版 数学中国网



1



球体表面积 球的体积和表面积 图文 叽叽歪歪吧



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



祖暅原理牟合方盖 算个球的表面积
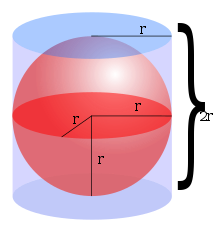



球面 维基百科 自由的百科全书
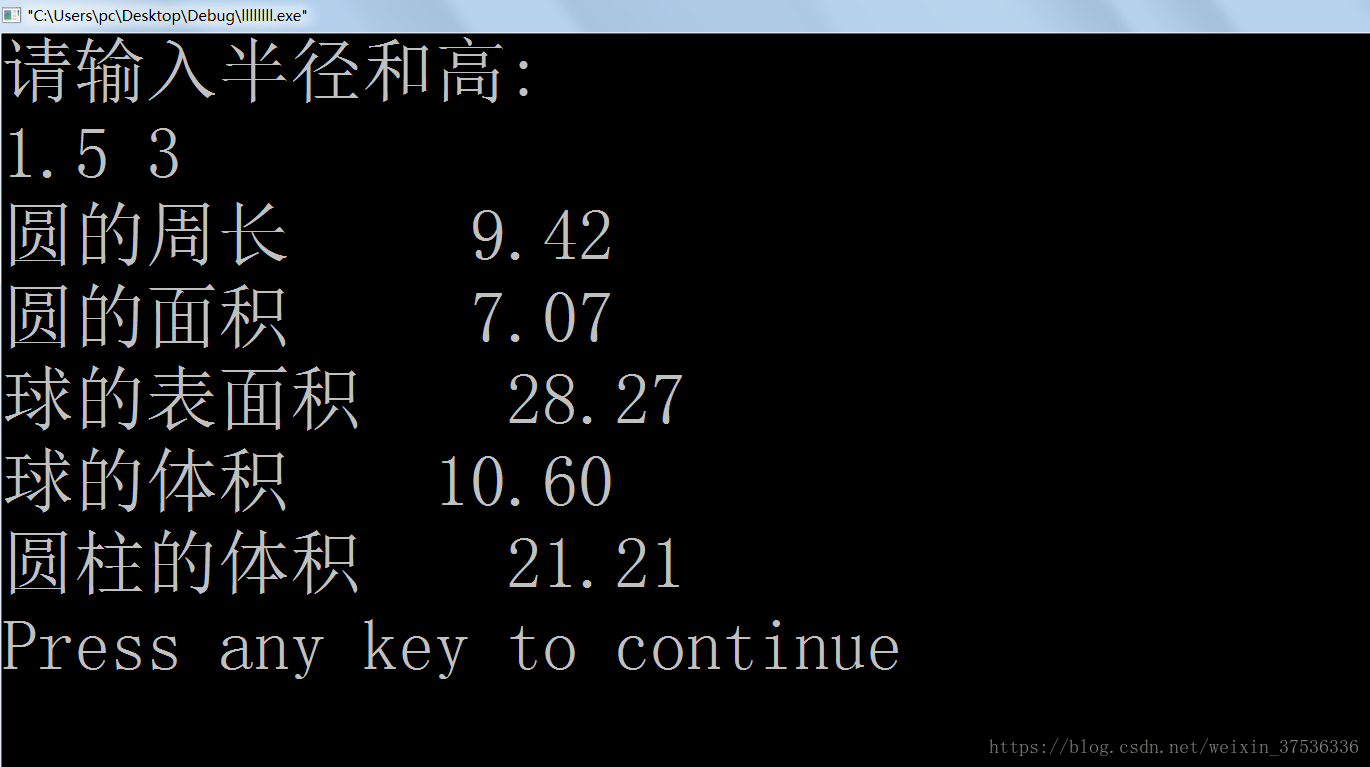



圆半径r 1 5 圆柱高h 3 求圆周长 圆面积 圆球表面积 圆球体积 圆柱体积 希望能对学习c语言的朋友有帮助 程序员宅基地




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




球体体积 球体表面积公式 球体体积公式 简明教程



0 件のコメント:
コメントを投稿