難易度:★★★★★☆算オリ・灘中受験生レベル 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 点( )は半径6cmの円のまわりを12等分する点です。三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。円の面積=∫(微小三角形の面積) 微小三角形の面積は図より 1 2 rdr= 1 2 r (rdθ)

三角形の内接円 三角形の面積を求める公式の証明 数学i By ふぇるまー マナペディア
円 三角形 面積 中学
円 三角形 面積 中学-はじめに 半径 r r の円の面積は πr2 π r 2 ですから、半径1の円の面積は π π です。 従って、半径1の円に内接する4角形, 8角形, 16角形 の面積は 円周率 π π に近づいてゆくはずです。 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の16角形が得られ、以下同様に 32角形, 64角形円の半径を計算し、円の面積を求めてみましょう。 はじめに、直角三角形の辺の比を確認してください。直角二等辺三角形の辺の比は、√2:1:1 です。また、60°と30°を内角にもつ直角三角形の辺の比は、2:1:√3 で



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
数学の問題です。 半径aの円に内接する三角形があります。 この三角形の各辺の中点を通る円があります。 この円の面積をaを使って表して下さい。 / 三角形の相似を使う問題ですね。 最初の円の面積の1/4になるでしょう。 これは中学生の宿題ではないのですか?S=rs となります 三角形の面積は,いろんな求め方がありますそこで, ヘロンの公式など を用いて三角形の面積を求めておくと,内接円の半径が求まります ヘロンの公式 三辺の長さが a , b , c である三角形の面積 S を求めるには まず、 s= ab三角形の面積 St 面積比 Sc/St お客様の声 アンケート投稿 よくある質問 リンク方法 三角形の外接円 110 /15件 表示件数 1 1123 50歳代 / 会社員・公務員 / 役に立った / 三角形の3辺から外接する円の半径と面積を計算します。
三角形の面積の公式 三角形の面積の公式といえば、 (底辺)×(高さ)÷2 で、お馴染みである。 基本的に、面 積の公式は全て、この公式が出発点である。 例1.の変形バージョンとしては次の公式が有名だろう。 ただし、sは、三角形の周の長さの半分正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)1 2 A B C A B C A A b c b c H H 図の ABCで辺ABに対する高さCHはどちらもb sinAである。 よって ABCの面積Sは S = 1 2 bc sinAとなる
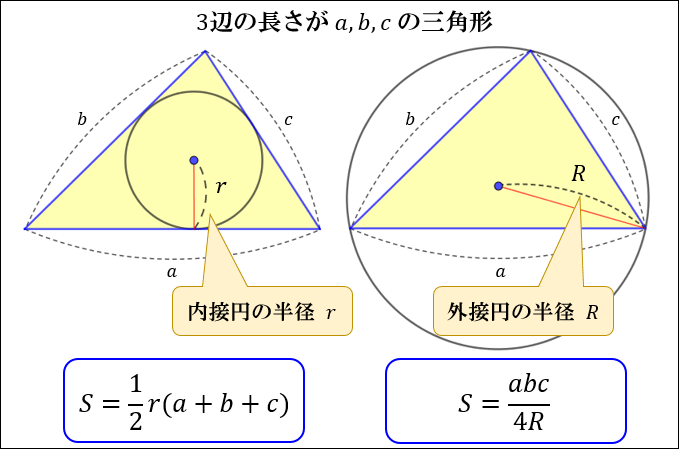
単位円に内接する正三角形の面積は 3 3 / 4 です。152 Studies in Science and Technology, V5221 S = N (N – A) (N – B) (N – C) (4) さらに、図4のように、外接円の半径Rと三つの角度α、β、 γが分かっている三角形の面積Sは式(5)で求められる。 S =2R2 sin α β γ (5) 5図 のように、内接円の半径rと三辺の総和Lが分かってい る三角形の面積Sは式(6)で求め② 三角形の面積の変 化や,直径と円周 の関係を表や式に 表している。 ③ 円周率を用いて円 や直径の長さを計 算できる。 ① 三角形や平行四辺 形,円がどんな図 形で構成されてい るか理解する。 ② 三角形・平行四辺 形・円の面積を求 める公式を理解



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



三角形の内接円 Geogebra
面積 1辺の長さから正三角形の面積,周囲の長さ,高さを計算します。 底辺と高さから三角形の面積を計算します。 2辺とその間の夾角から三角形の面積、周囲の長さ、高さを計算します。 3辺から三角形の面積をヘロンの公式を使って計算します。 1辺と正三角形の面積の公式・求め方について慶応大学に通う筆者が丁寧に解説 します。 数学が苦手な人でも正三角形の面積の公式・求め方が理解できるよう、スマホでも見やすいイラストを使いながら解説します。 正三角形の面積の公式を暗記していれば、問題もすぐに解くことができます9th STAGE 14 正三角形と円と扇形が作る図形の面積 直径6の半円と、1辺が6の正三角形。 半円の直径と三角形の底辺が共通。 右下の三角形も、左下の三角形も、 1辺が3の正三角形になりそうですが、、、。 そのことの証明と、あとはどの図形とどの図形を



中学の数学の図形問題についてお聞きします 1辺の長さが10cmの正三角形と Yahoo 知恵袋
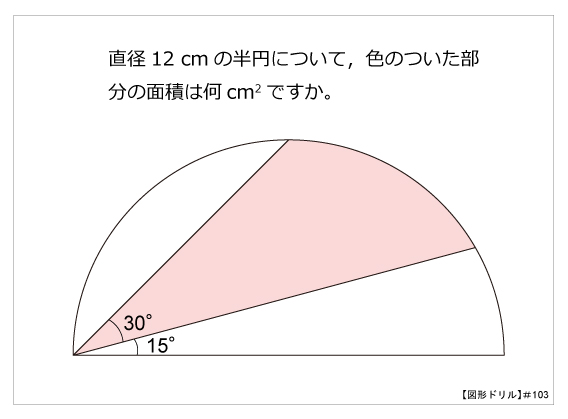



半円 算数星人のweb問題集 中学受験算数の問題に挑戦
三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する三角形の面積との関係 内接円と傍接円の半径は、三角形の面積に関係している。 S を三角形の面積、a, b, c を3辺の長さ、s を半周長としたとき、ヘロンの公式から、 = ( ) () () () = () 一方、内接円の半径は、 = () 辺 a に対する傍接円の半径は、 となる。 他の2辺に対する傍接円の半径は2 = 半 径 ×



1
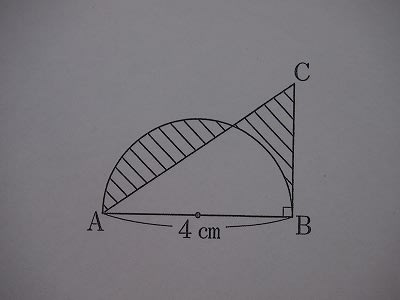



15年2月のブログ記事一覧 マッキーのつれづれ日記
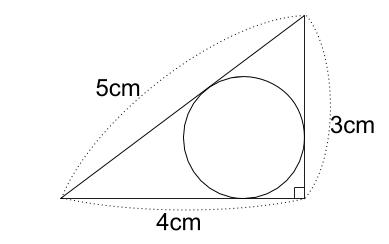
直角三角形の場合 図のような、各辺の長さが 3 、 4 、 5 である直角三角形の内接円の半径を求めよ。 三角形の面積は、 3 ×2 = 6 です。円周率 底 辺 ×
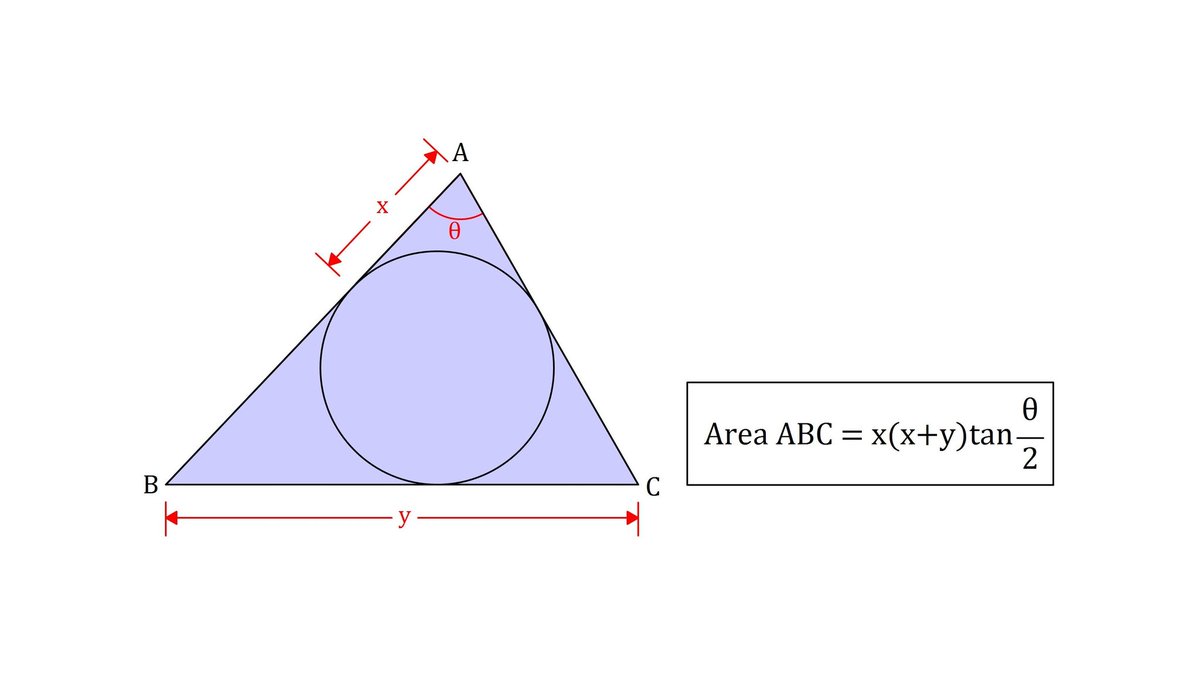



ポテト一郎 Di Twitter 円に外接する三角形の面積




算数 直角三角形に内接する円と面積の問題 なるほどの素
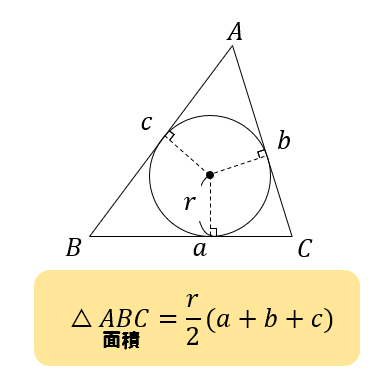
三角形ABCの面積をS、外接円の半径をRとするとき、 次の等式が成り立つことを証明せよ。 1S=2R^2sinAsinBsinC 2S=abc/4R という問題です よろしくおねがいします。三角形の面積を使って内接円の半径を求める 内接円の半径を r とおきます。 内接円の半径を求める公式 より、 r = 2S a b c です。 また、 正三角形の面積の求め方 より、 S = √3 4 a2 が成立します。 よって、 r = 2 ×内接円とは,三角形の3つの辺全てに接する円のこと。 内接円の半径は, S = r 2 ( a b c) S=\dfrac {r} {2} (abc) S = 2r (a b c) という公式を使って計算することができる。 三角形の内接円について詳しく解説します。 前半では,内接円の半径の計算公式の




円弧面積の計算式




三角形の内接円 三角形の面積を求める公式の証明 数学i By ふぇるまー マナペディア
その円の上に三角形abcをおき、黄色い辺bcを固定して、頂点aを動かします。 いま、頂点Aを点A'のところまで動かしました。 頂点Aを円周上で動かしていくと、円周角がもとの値(home angle)から変化するのが見られます。S = 1 2 r ( a b c) 「3辺の長さ a, b, c 、外接円の半径 R の三角形」の面積は S = a b c 4 R で求められます。 ただ、これらの公式を使わなくても3辺の長さ a, b, c の値が分かっている時点で「④ ヘロンの公式」を使えば三角形の面積を求めることは可能です2 = 直 径 ×




円の面積
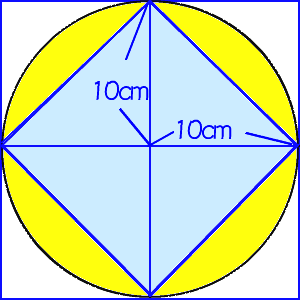



6年算数 円の面積 1 アニメでわかる教え方
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題√3 4 a2 a a a = √3 6 aし,円の面積などを 求めることができ る。 技 ノート 察 ひ も を 使 っ て 円 の 面 積 を 確 か め よ う ( 1 ) 。 ま ひもで作 った円を 三角形にすることよて, の面積の公式から円の面積の公式を導き出す。 三角形の面積の 公式から円の面積 の公式



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典



1
また、三角形の面積Sは以下の式であらわせる。 (式3) 2S=ah 式3に式2を代入してhを消去する。 2S=abc/(2R) S=abc/(4R) (解答おわり) リンク: 三角形の面積(二辺侠角) 三角形の面積と内接円の半径円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円三角形の外接円の半径、内接円の半径と面積の関係 S=1/2r(abc) 三角形の頂角の二等分線の長さ:基本2パターン、裏技公式 x=√(abcd) とその証明 中線定理(パップスの定理)とスチュワートの定理の三角比による証明




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット
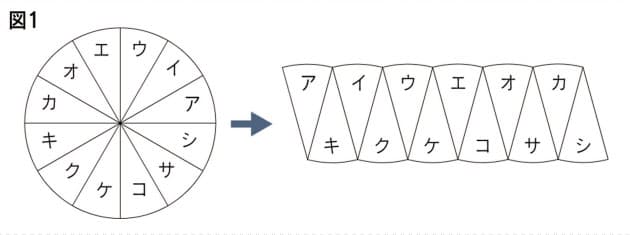



子供に説明できる 円の面積の公式 の証明 Nikkei Style
正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)円 周 率 ×この面積公式をもとに他の面積公式を導出することができます。 例えば,この公式と正弦定理を用いることで対称な式: S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます( R R R は三角形 A B C ABC A BC の外接円の半径)。→外接円の半径と三角形の面積
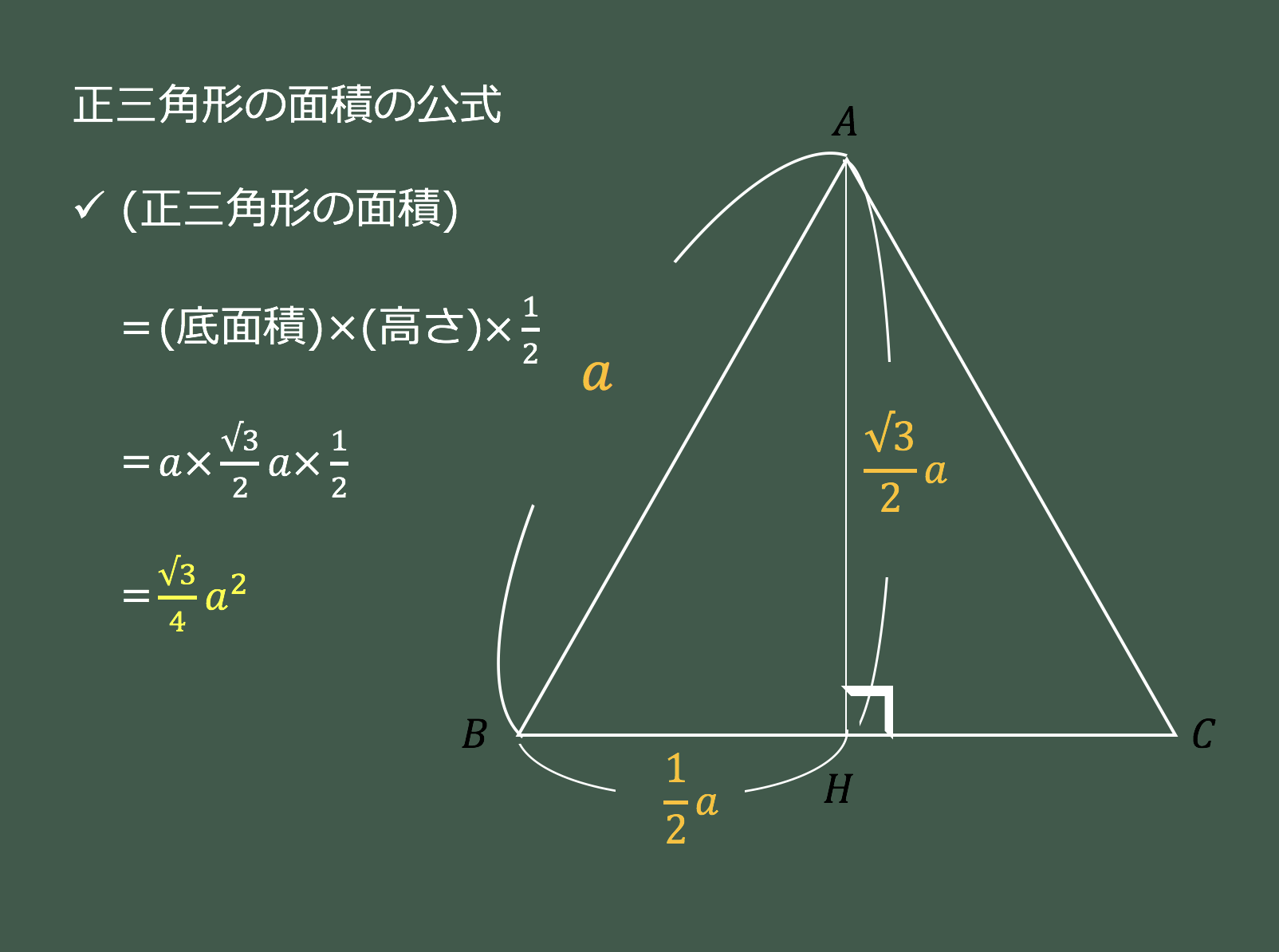



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ
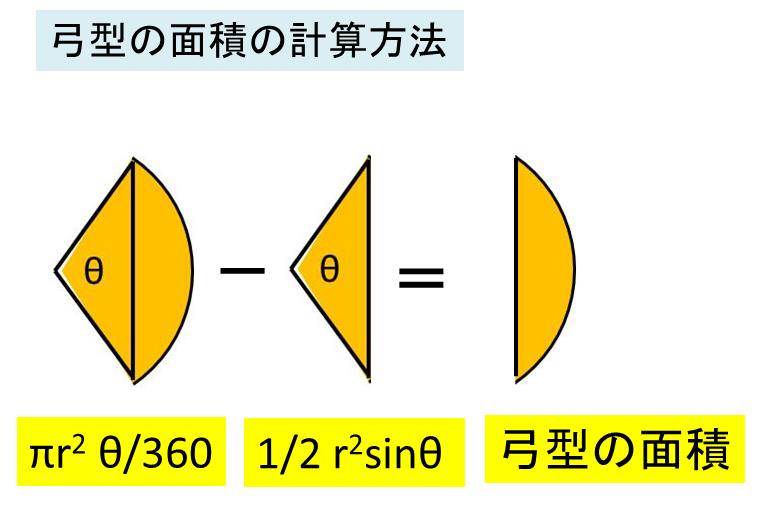



欠けた円 欠円 や弓形の面積の計算方法
円とおうぎ形⑹ 弓形の面積 23 解説 1 おうぎ形から直角二等辺三角形を引く 1 =16×π−32 =5024−32 =14(㎠) 弓形の面積=おうぎ形−直角二等辺三角形 2 赤いおうぎ形−斜線の三角形 1 =456(㎠) 3 斜線の弓形を求めて2倍する 1




円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト
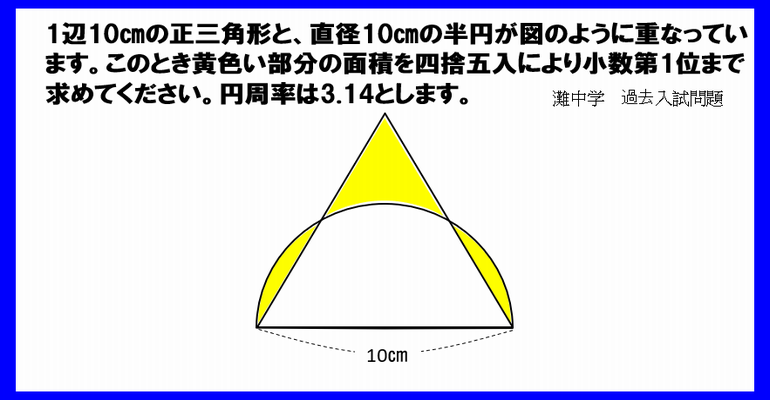



算数問題 全2問 中学入試で出題された難問 子供から大人まで動画で脳トレ 楽天ブログ




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月
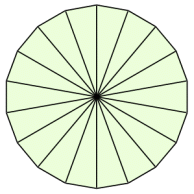



積分 円の面積の再考 大人が学び直す数学




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



三角形とその内接円 および外接円の面積について考えてみる 内接円は 三角形のそれぞれの角の二等分線の交点から 各辺に垂線を降ろした線分を半径とした円です 内接円の半径 R は それぞれの角の二等分線より であり すべての R は




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ




斜線部の面積を求める 1 Youtube
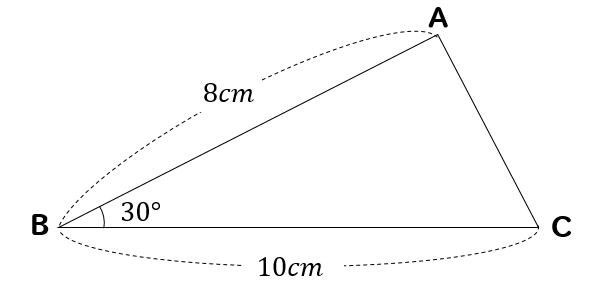



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
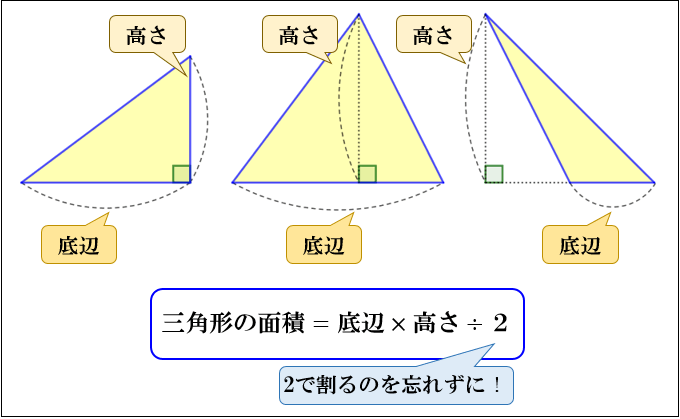



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
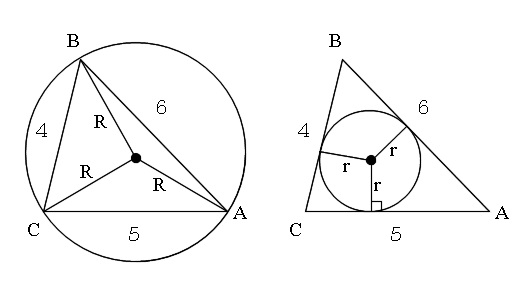



正弦定理と余弦定理の使い方と面積の公式




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




円に内接する三角形の面積 解答編 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング
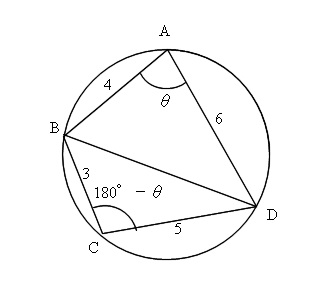



円に内接する四角形の面積の求め方と定理の使い方
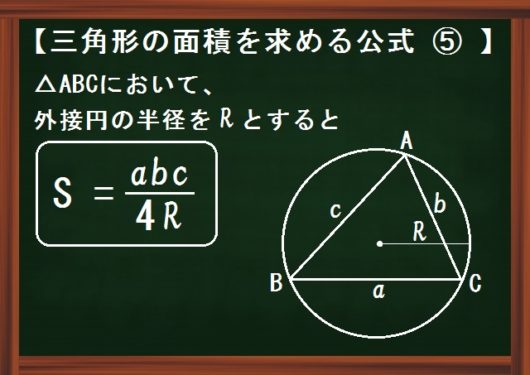



三角形の面積を求める公式7選 高校数学のまとめにどうぞ



単位円上にある異なる3点がつくる三角形の面積の最大値をどう求めますか Quora
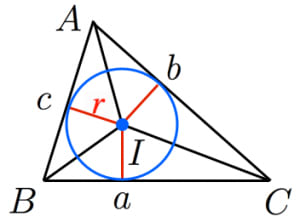



内接円の半径と三角形の面積 高校数学の美しい物語




三角形の面積を外接円の半径を使って求める Schoolmath S Diary




中学受験算数 まいにち算数078 円の通過面積 02年灘中 勉強 Youtube スタディチューブ
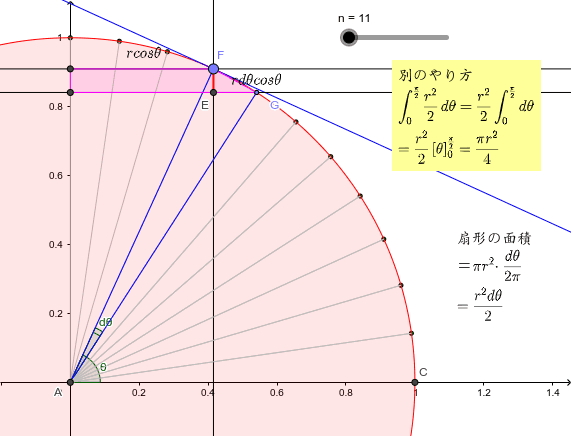



円の面積2 Geogebra




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
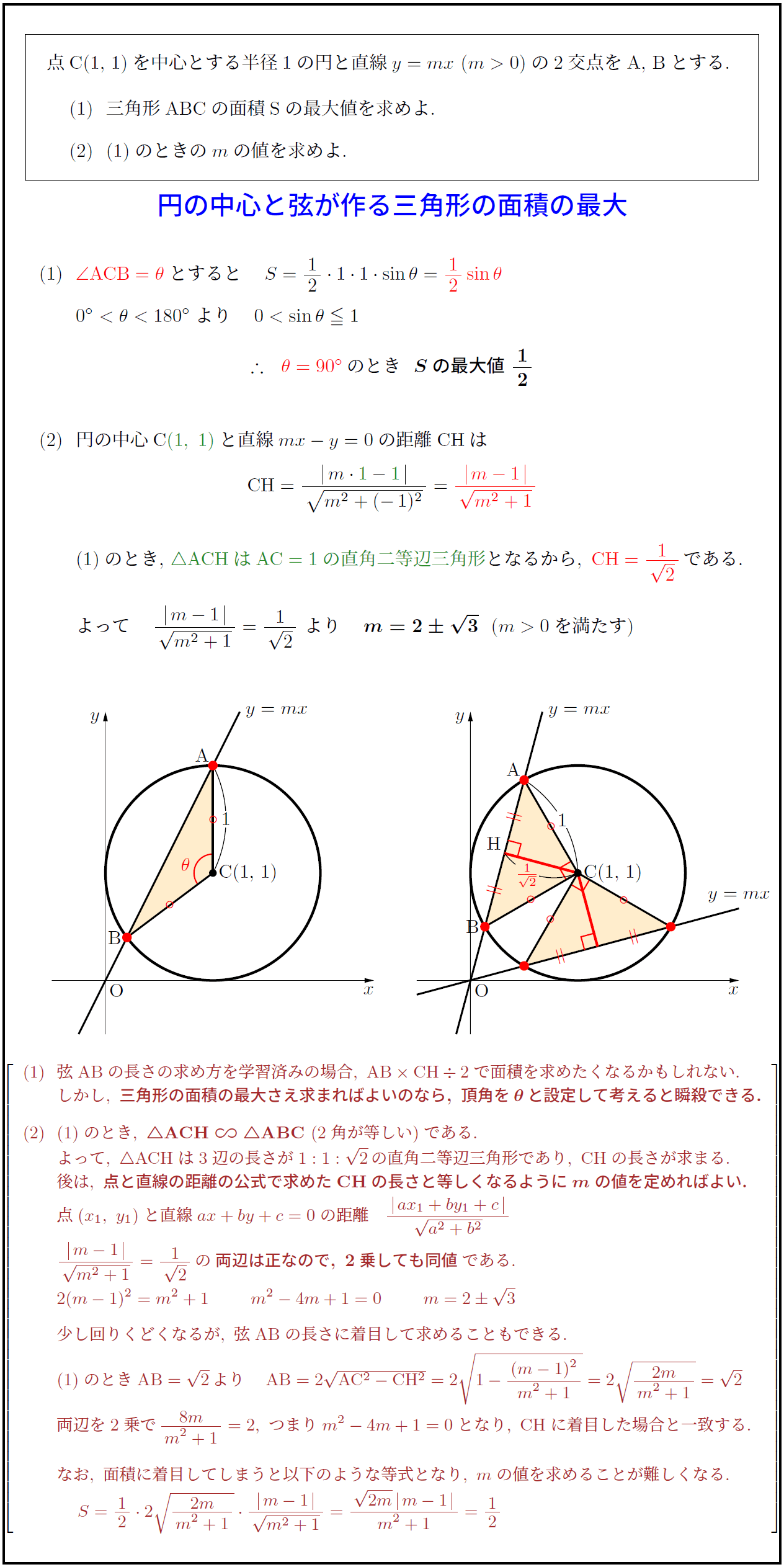



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月
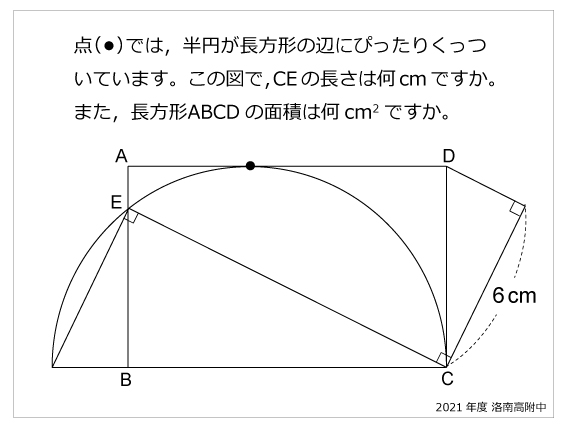



半円 算数星人のweb問題集 中学受験算数の問題に挑戦
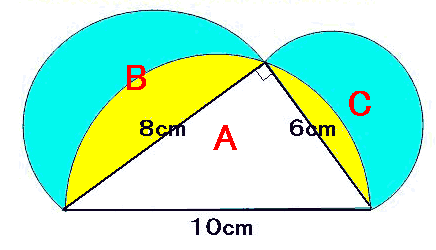



算数 三日月形 半円 の面積の応用問題の答 なるほどの素
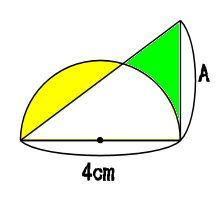



円と三角形




同じ広さはどこ 半円と正三角形 Geogebra



小学6年生の娘の宿題 図の灰色部分の面積を求めよ という問題です Yahoo 知恵袋




三角形の外接円の面積 奈良県立 数学カフェjr



外接円とは 半径の公式や求め方 性質 書き方 受験辞典




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ



48s96ub7b0z5f Net Sankaku Menseki




2 の三角形の断面と下の半円の面積は求められるのですが扇形の面積が求められません Clear



三角形の内接円 中学数学の無料オンライン学習サイトchu Su



Excel Vba 数学実験室 正三角形と内接する円の面積比




三角形の面積は 講師ブログ



Excel Vba 数学実験室 2 等辺三角形に外接する円の面積




2 の三角形の断面と下の半円の面積は求められるのですが扇形の面積が求められません Clear




例題 三角形の面積と内接円 Youtube




面積の求め方 計算公式一覧
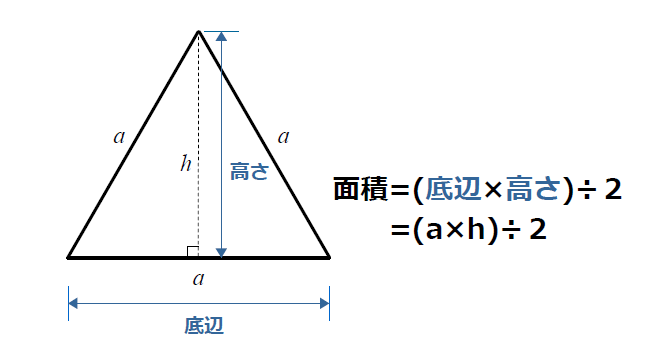



正三角形の面積計算 ゆるゆるプログラミング



3




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数



多角形の面積で円周率を求める Allisone



しょうちゃん 公式ブログ 算数の問題を解いてみる その13 図形 Powered By Line




外接円の半径と三角形の面積の関係 S Abc 4r 高校数学の美しい物語




民報チャレンジ18 数学15 図形の面積 N Kaneta Blog
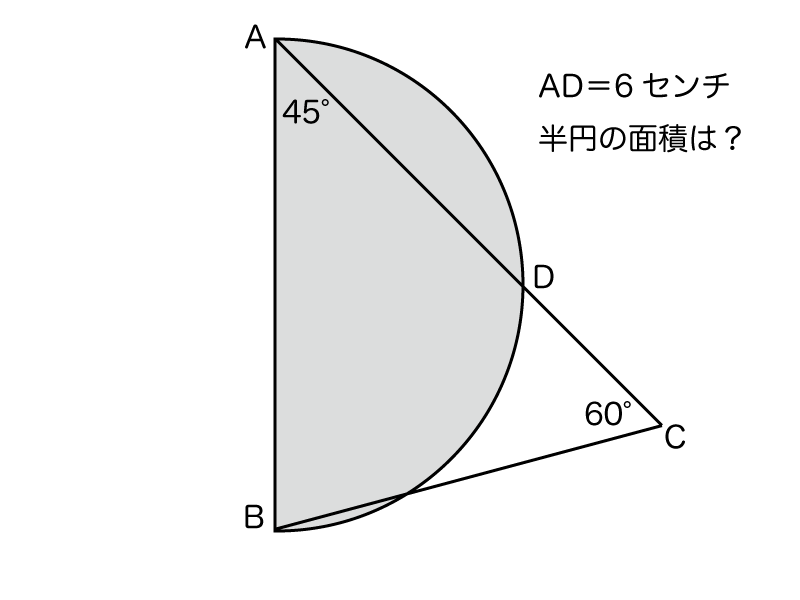



面積公式を組み合わせて解く半円の面積計算 受験算数入門
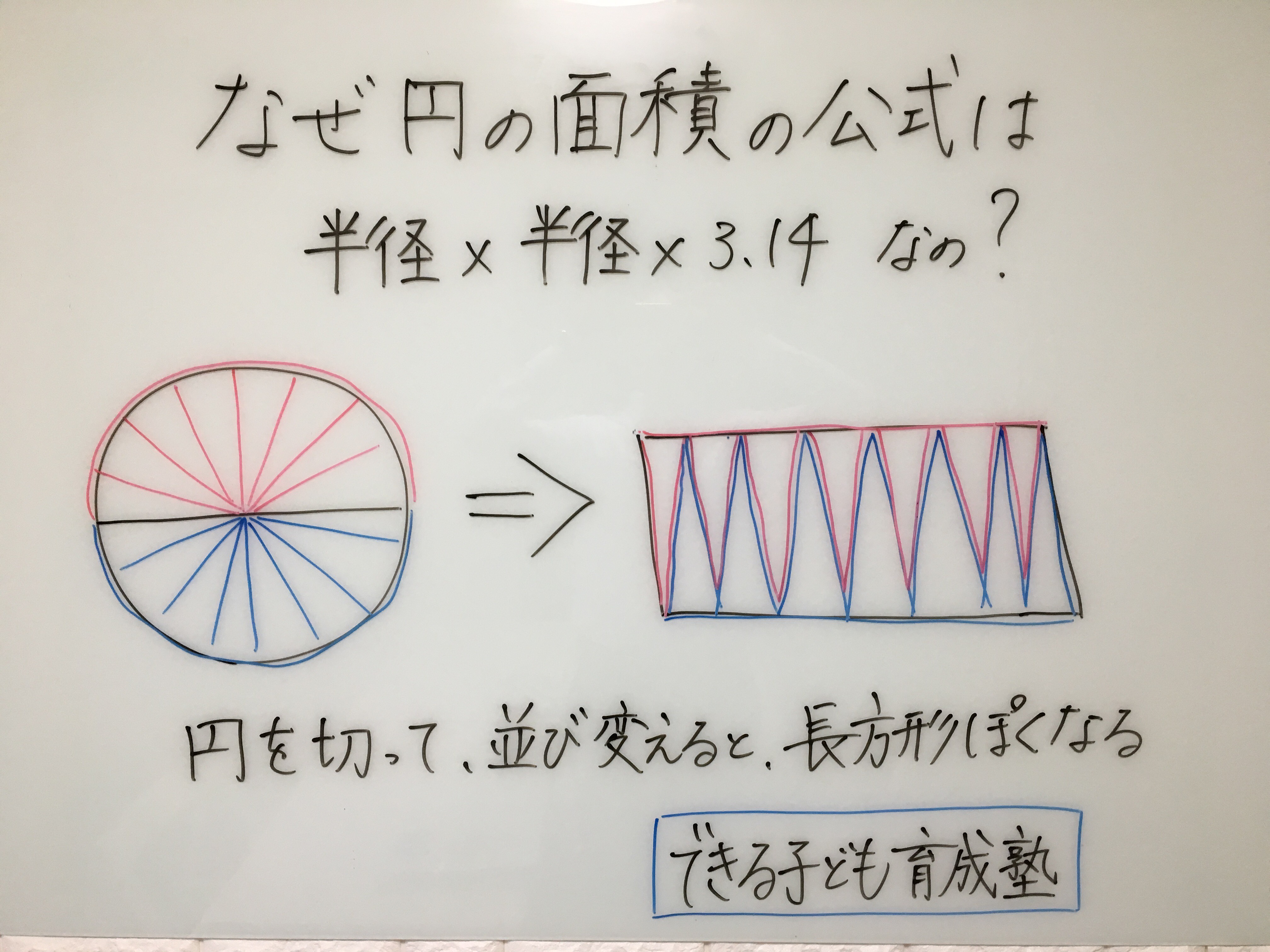



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




数学ia 三角形の内接円と外接円 大学入試数学の考え方と解法
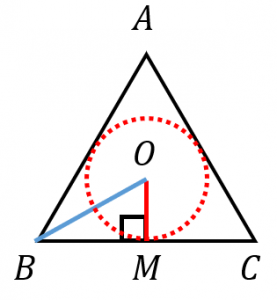



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数
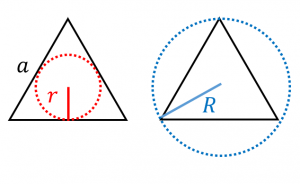



正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学



円 三角形の面積 中学から数学だいすき




円の面積



教えて下さい 下記の図はアイを直径とする半円と直角三角形アイウ Yahoo 知恵袋



円と直角三角形 鴎友学園女子中学 2010年 どう解く 中学受験算数




中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー




中学受験算数 等積変形の利用 ヒポクラテスの月




超頻出 正三角形の中にある正三角形の面積 問題 恋する中学受験 大学受験を見据えた中学受験



雑学のソムリエ 正三角形の中の円の中の正三角形
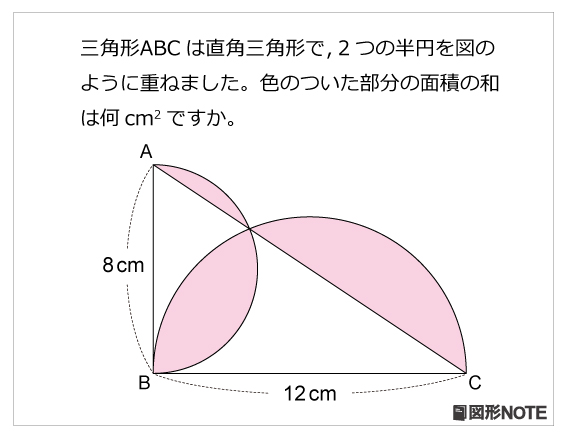



半円 算数星人のweb問題集 中学受験算数の問題に挑戦




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学の伝道師 秋山仁さん 算数を勉強しないと損 子どもを算数好きに育てるには 親子で挑む 算数つまずき攻略法 朝日新聞edua




半円と直角三角形 算数の広場



三角形の面積から逆算 図形と計量 おおぞらラボ




円に内接する正三角形の問題 社会人になり勉強することもなくなったの 数学 教えて Goo
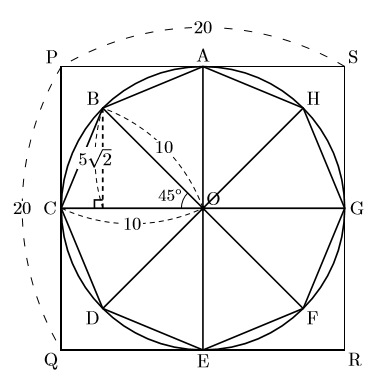



中学数学 円周率は3より大きいの証明 数樂管理人のブログ



1




327 三角形の面積 内接円 Youtube
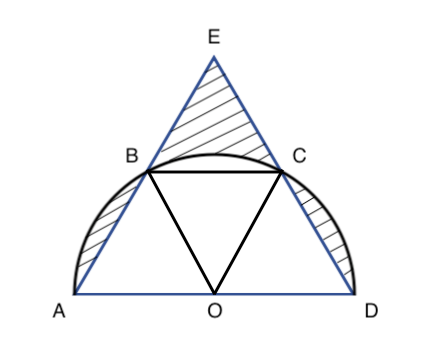



斜線部分の面積を求める問題 よくあるパターン 苦手な数学を簡単に
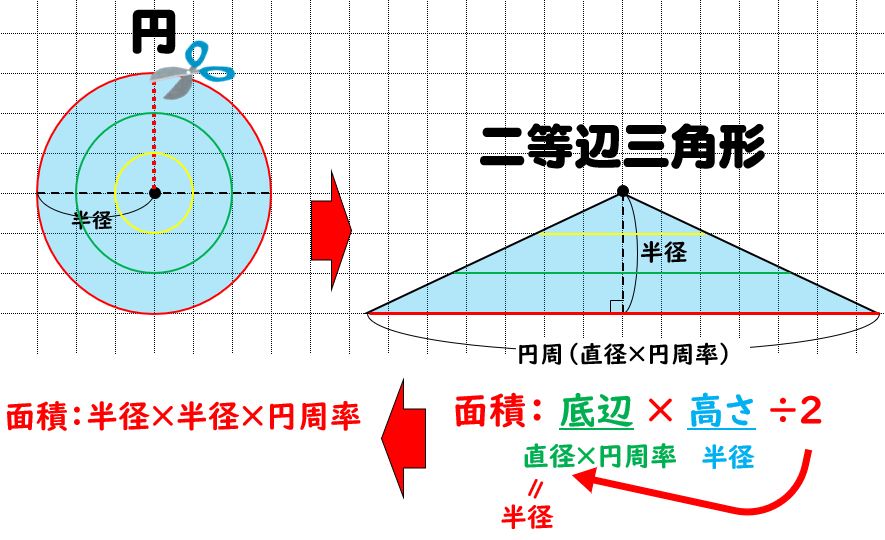



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




三角形の外接円の 4 つの性質 証明付 理数アラカルト




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora




円の面積4 円の面積を求める別の方法 身勝手な主張



9th Stage 14 正三角形と円と扇形が作る図形の面積 数学クイズ なん度 Math Quiz Find Angles




三角形の面積を求める方法は何通り その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
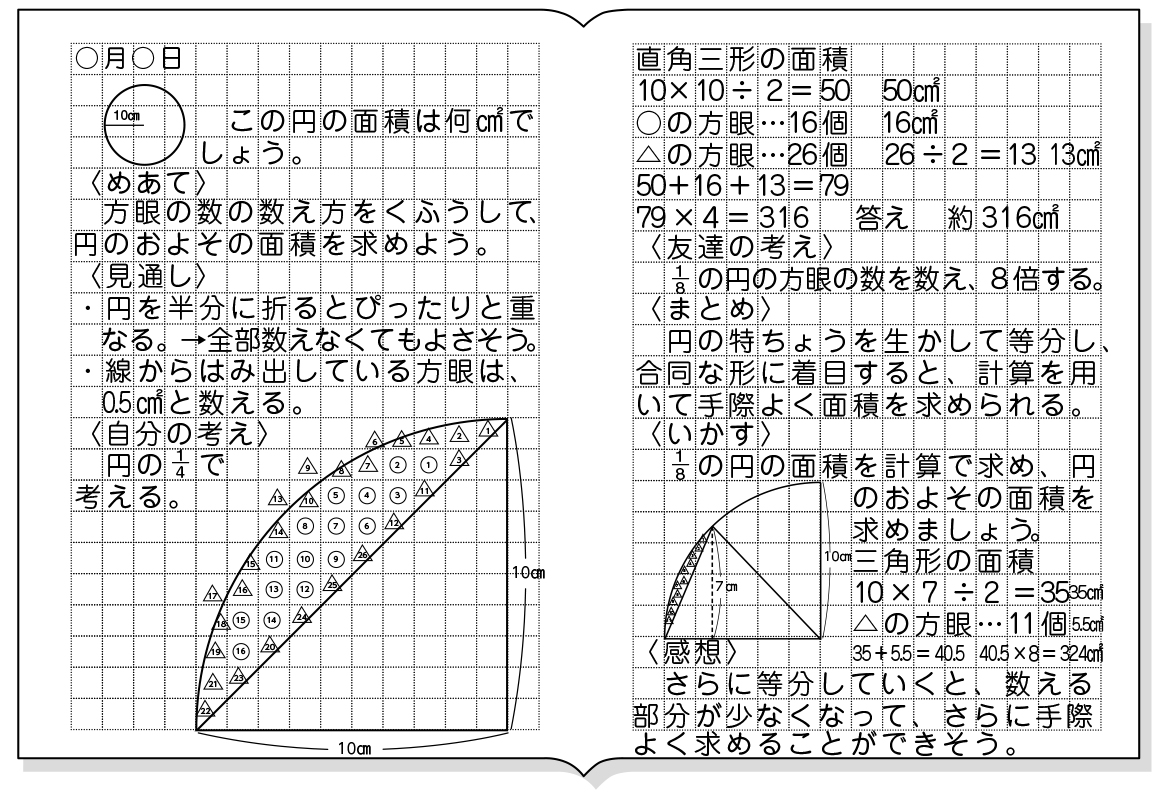



小6算数 円の面積 指導アイデア 1 みんなの教育技術



0 件のコメント:
コメントを投稿